
����Ŀ��Ϊ�������꼶ѧ����ѧϰ�ɼ�״������Ӧ�Լ����������п����ý�ѧ������ij��ѧ��ȡ�˲��ֲμӿ��Ե�ѧ���ijɼ���Ϊ�������������Ƴ�������������������ͳ��ͼ�������ͼ���ṩ����Ϣ����������⣺
��1������ѧ�ɼ����Ϊ���С���������
��2���������ͼ�У����š���ռ�İٷֱȣ���������ͳ��ͼ����������
��3����У���꼶����1000�˲μ�����ο��ԣ�������У���꼶���ж�����ѧ������ѧ�ɼ��ﵽ���㣿
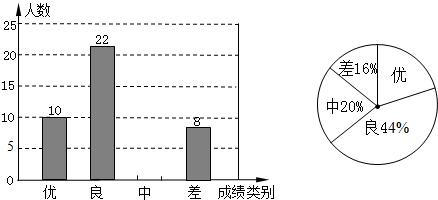
���𰸡�(1) 10�ˣ�(2)��������(3)200��
��������
��1����������������ռ�İٷֱȵõ������������������20%���ɵõ������
��2���ɼ����Ϊ��������������ռ�İٷֱ�=�ɼ����Ϊ������������������ȡ��ѧ���������ɣ�1�������������ɲ�ȫ����ͳ��ͼ��
��3��У���꼶ѧ������ѧ�ɼ��ﵽ���������=1000���ɼ����Ϊ��������ѧ����ռ�İٷֱȣ�
��1��22��44%��20%=10���ˣ���
�������б�ʾ�ɼ����Ϊ��������������10�ˣ�
��2������ͼ�У���������ռ�İٷֱ�Ϊ1-��44%+20%+16%��=20%��
��ȫ��ͼ����ͼ��ʾ��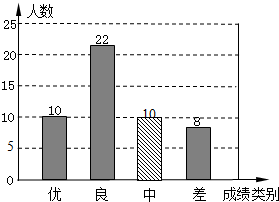
��3��1000����1-16%-44%-20%��=200���ˣ���
����Ƹ�У��һ��������80��ѧ���ijɼ����Դﵽ���㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�ֱ��y=��![]() x+
x+![]() ��x�ύ�ڵ�A����y�ύ�ڵ�B��������y=ax2+bx+
��x�ύ�ڵ�A����y�ύ�ڵ�B��������y=ax2+bx+![]() ��a��0����A��B���㣬��x�ύ����һ��C����1��0���������ߵĶ���ΪD��
��a��0����A��B���㣬��x�ύ����һ��C����1��0���������ߵĶ���ΪD��
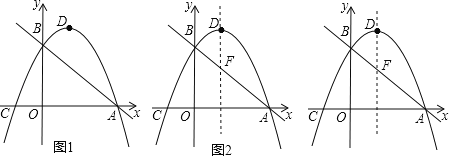
��1�����A��B��������ꣻ
��2���������ߵĽ���ʽ������D�����ꣻ
��3����ֱ��AB�Ϸ�������������һ����E�������E��ֱ��AB�ľ�������ֵ��
��4����ͼ2��ֱ��AB�������ߵĶԳ����ཻ�ڵ�F����P���������ϣ��ҵ�P��ֱ��BD��DF�ľ�����ȣ���ֱ��д����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪����ABC����C��90����BC��3��AC��4.��C�İ뾶��Ϊ1����֪��P����ABC����һ���㣨�����붥���غϣ�
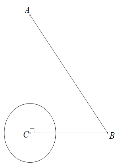
��1������P����C�����߳�Ϊ![]() ����AP�ij���Ϊ ��
����AP�ij���Ϊ ��
��2������P����C�����߳�Ϊm�����P��λ���м�������ֱ��д�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��l��y����1��������L��y��ax2+bx+c��a��0����������L�Ķ���Ϊԭ�㣬�Ҿ�����A(2![]() ,
,![]() )��ֱ��y��kx+1��y�ύ�ڵ�F����������L���ڵ�B��x1��y1����C��x2��y2������x1��x2��
)��ֱ��y��kx+1��y�ύ�ڵ�F����������L���ڵ�B��x1��y1����C��x2��y2������x1��x2��
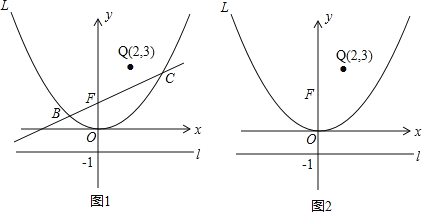
��1����������L�Ľ���ʽ��
��2����P��������L��һ���㣮
���Ե�PΪԲ�ģ�PFΪ�뾶����P�����жϡ�P��ֱ��l��λ�ù�ϵ����˵�����ɣ�
������Q��2��3������|PQ��PF|��ֵ��Сʱ�����P�����ꣻ
��3����֤������kΪ��ֵ��ֱ��l��������BCΪֱ����Բ���У�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ǹ������¶��壺˳����������һ���ı��θ����е����õ��ı��ν��е��ı��Σ�
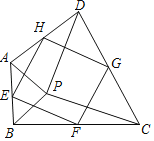
��1����ͼ����P���ı���ABCD��һ�㣬������PA��PB��PC��PD����APB����CPD����E��F��G��H�ֱ�Ϊ��AB��BC��CD��DA���е㣬�����е��ı���EFGH����״����֤����IJ��룻
��2�����ı䣨1���е�������ʹ��APB����CPD��90���������������䣬ֱ��д���е��ı���EFGH����״������֤������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����6�֣���һ��������ֽ����װ�к졢�ơ���������ɫ��С�����dz���ɫ����ȫ��ͬ�����к�����2����������1����������1��.����һ�ŵ�ӰƱ��С����С������ͨ��������Ϸ����Ӯ��Ӯ��һ���õ�ӰƱ������Ϸ�����ǣ����˸���1��������С����ֽ�����������1����¼��ɫ��Żأ���С��ҡ�ȣ�����С���������1����¼��ɫ������������������ɫ��ͬ����С��Ӯ������С��Ӯ�������Ϸ�����˫����ƽ������������״ͼ���б���˵������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У�AC��a��BD��b����AC�ABD��˳�������ı���ABCD�����е㣬�õ��ı���A1B1C1D1����˳�������ı���A1B1C1D1�����е㣬�õ��ı���A2B2C2D2������˽�����ȥ���õ��ı���AnBnnDn�����н�����ȷ���У�������
���ı���A2B2C2D2�Ǿ��Σ�
���ı���A4B4C4D4�����Σ�
���ı���A5B5C5D5���ܳ���![]()
���ı���AnBnnDn�������![]() ��
��

A.�٢�B.�ڢ�C.�ڢۢ�D.�٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ���߳��ֱ�Ϊ8��16�ľ���ֽƬABCD��EF�۵���ʹC����A���غϣ���EF��AF�ı�ֵΪ�� ��

A.4 ![]() B.
B.![]() C.2D.
C.2D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ������![]() ��
��![]() ��
��![]() (
(![]() )�ĺ���ֻ������(����)
)�ĺ���ֻ������(����)
A.����������B.һ�κ���C.����������D.���κ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com