
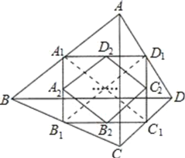
【题目】如图,四边形ABCD中,AC=a,BD=b,且AC丄BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2…,如此进行下去,得到四边形AnBnnDn.下列结论正确的有( )
①四边形A2B2C2D2是矩形;
②四边形A4B4C4D4是菱形;
③四边形A5B5C5D5的周长是![]()
④四边形AnBnnDn的面积是![]() .
.

A.①②B.②③C.②③④D.①②③④
【答案】C
【解析】
①由两组对边平行,证明出A1B1C1D1是平行四边形,再根据四边都相等,证明出是菱形.
②由①知四边形A2B2C2D2是菱形,根据中位线定理,四边形A4B4C4D4是菱形.
③根据中位线性质得到每边长的关系,从而计算出周长.
④三角形的中位线的性质可以推知,每得到一次四边形,它的面积变为原来的一半.
①连接A1C1,B1D1.
∵在四边形ABCD中,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1,
∴A1D1∥BD,B1C1∥BD,C1D1∥AC,A1B1∥AC;
∴A1D1∥B1C1,A1B1∥C1D1,
∴四边形A1B1C1D1是平行四边形;
∵AC丄BD,∴四边形A1B1C1D1是矩形,
∴B1D1=A1C1(矩形的两条对角线相等);
∴A2D2=C2D2=C2B2=B2A2(中位线定理),
∴四边形A2B2C2D2是菱形;
故①错误;
②由①知,四边形A2B2C2D2是菱形;
∴根据中位线定理知,四边形A4B4C4D4是菱形;
故②正确;
③根据中位线的性质易知,A5B5=![]() A3B3=
A3B3=![]() ×
×![]() A1B1=
A1B1=![]() ×
×![]() ×
×![]() AC,B5C5=
AC,B5C5=![]() B3C3=
B3C3=![]() ×
×![]() B1C1=
B1C1=![]() ×
×![]() ×
×![]() BD
BD
∴四边形A5B5C5D5的周长是2×![]() (a+b)=
(a+b)=![]() ;
;
故③正确;
④∵四边形ABCD中,AC=a,BD=b,且AC丄BD,
∴S四边形ABCD=ab÷2;
由三角形的中位线的性质可以推知,每得到一次四边形,它的面积变为原来的一半,
四边形AnBnnDn的面积是![]() ;
;
故④正确;
综上所述,②③④正确.
故选:C.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
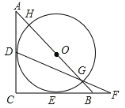
【题目】如图,△ABC是等腰直角三角形,AC=BC=2,以斜边AB上的点O为圆心的圆分别与AC、BC相切于点D、E,与AB分别相交于点G、H,且DG的延长线与CB的延长线交于点F,分析下列四个结论:①HG=2;②BG=BF;③AH=BG=![]() ;④CF=
;④CF= ![]() .其中正确的结论个数有( )
.其中正确的结论个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
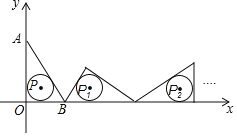
【题目】如图,把Rt△OAB置于平面直角坐标系中,点A的坐标为(0,4),点B的坐标为(3,0),点P是Rt△OAB内切圆的圆心.将Rt△OAB沿y轴的正方向作无滑动滚动.使它的三边依次与x轴重合.第一次滚动后,圆心为P1,第二次滚动后圆心为P2…依次规律,第2019次滚动后,Rt△OAB内切圆的圆心P2019的坐标是( )
A.(673,1)B.(674,1)C.(8076,1)D.(8077,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
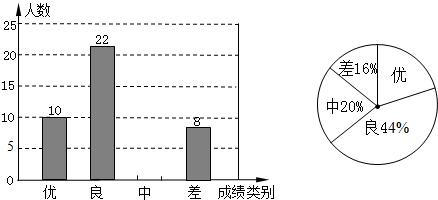
【题目】为评估九年级学生的学习成绩状况,以应对即将到来的中考做好教学调整,某中学抽取了部分参加考试的学生的成绩作为样本分析,绘制成了如下两幅不完整的统计图,请根据图中提供的信息解答下列问题:
(1)求本中学成绩类别为“中”的人数;
(2)求出扇形图中,“优”所占的百分比,并将条形统计图补充完整;
(3)该校九年级共有1000人参加了这次考试,请估算该校九年级共有多少名学生的数学成绩达到优秀?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
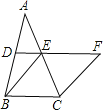
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解方程。
(1)4(x-3) ![]() =36
=36
(2)x2-4x+1=0.
(3)![]() -7x+6=0
-7x+6=0
(4)![]()
(5)(y-1)2+2y(1-y)=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
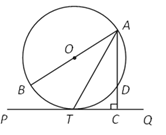
【题目】如图,![]() 为⊙O的直径, D、T是圆上的两点,且AT平分∠BAD,过点T作AD延长线的垂线PQ,垂足为C.
为⊙O的直径, D、T是圆上的两点,且AT平分∠BAD,过点T作AD延长线的垂线PQ,垂足为C.
(1)求证:PQ是⊙O的切线;
(2)若⊙O的半径为2,![]() ,求弦AD的长.
,求弦AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(1,1),B(3,1),C(3,﹣1),D(1,﹣1)构成正方形ABCD,以AB为边做等边△ABE,则∠ADE和点E的坐标分别为( )

A. 15°和(2,1+![]() )
)
B. 75°和(2,![]() ﹣1)
﹣1)
C. 15°和(2,1+![]() )或75°和(2,
)或75°和(2,![]() ﹣1)
﹣1)
D. 15°和(2,1+![]() )或75°和(2,1﹣
)或75°和(2,1﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
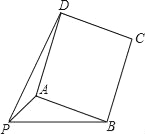
【题目】已知:PA=![]() ,PB=4,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.
,PB=4,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.
(1)如图,当∠APB=45°时,求AB及PD的长;
(2)当∠APB变化,且其它条件不变时,求PD的最大值,及相应∠APB的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com