
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
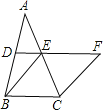
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
【答案】解:(1)证明:∵D、E分别是AB、AC的中点,∴DE∥BC且2DE=BC。
又∵BE=2DE,EF=BE,∴EF=BC,EF∥BC。
∴四边形BCFE是平行四边形。
又∵BE=FE,∴四边形BCFE是菱形。
(2)∵∠BCF=120°,∴∠EBC=60°。
∴△EBC是等边三角形。
∴菱形的边长为4,高为![]() 。
。
∴菱形的面积为4×![]() =
=![]() 。
。
【解析】
试题(1)从所给的条件可知,DE是△ABC中位线,所以DE∥BC且2DE=BC,所以BC和EF平行且相等,所以四边形BCFE是平行四边形,又因为BE=FE,所以四边形BCFE是菱形。
(2)因为∠BCF=120°,所以∠EBC=60°,所以菱形的边长也为4,求出菱形的高面积就可求。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
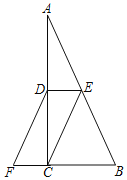
【题目】如图,在△ABC中,∠ACB=90°,点D、E分别是AC、AB的中点,点F在BC的延长线上,且∠CDF=∠A.
(1)求证:四边形DECF是平行四边形;
(2)若∠A=30°,写出图中所有与FD长度相等的线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
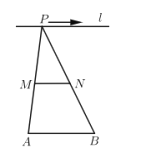
【题目】如图,点![]() 为定点,定直线
为定点,定直线![]() 是
是![]() 上一动点,点
上一动点,点![]() 分别为
分别为![]() 的中点,对于下列各值:①线段
的中点,对于下列各值:①线段![]() 的长;②
的长;②![]() 的周长;③
的周长;③![]() 的面积;④
的面积;④![]() 的大小.其中随点
的大小.其中随点![]() 的移动不会变化的是( )
的移动不会变化的是( )
A.①②B.①③C.①④D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某次运动会![]() 名运动员的年龄情况,从中抽查了
名运动员的年龄情况,从中抽查了![]() 名运动员的年龄,就这个问题而言,下列说法正确的是( )
名运动员的年龄,就这个问题而言,下列说法正确的是( )
A. ![]() 名运动员是总体 B. 每名运动员是个体
名运动员是总体 B. 每名运动员是个体
C. ![]() 名运动员是抽取的一个样本 D. 这种调查方式是抽样调查
名运动员是抽取的一个样本 D. 这种调查方式是抽样调查
查看答案和解析>>
科目:初中数学 来源: 题型:
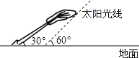
【题目】如图,太阳光线与地面成![]() 角,一棵倾斜的大树与地面成
角,一棵倾斜的大树与地面成![]() 角,这时测得大树在地面上的影长约为
角,这时测得大树在地面上的影长约为![]() ,则大树的长约为________
,则大树的长约为________![]() (保留两个有效数字,下列数据供选用:
(保留两个有效数字,下列数据供选用:![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
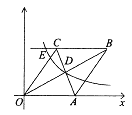
【题目】已知:如图在直角坐标系中,有菱形![]() ,
, ![]() 点的坐标为
点的坐标为![]() ,对角线
,对角线![]() ,
, ![]() 相交于
相交于![]() 点,双曲线
点,双曲线![]() 经过
经过![]() 点,交
点,交![]() 的延长线于
的延长线于![]() 点,且
点,且![]() ,则点
,则点![]() 的坐标为( )
的坐标为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
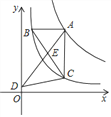
【题目】如图,点A是反比例函数y=![]() 图象上的任意一点,过点A作AB∥x轴,AC∥y轴,分别交反比例函数y=
图象上的任意一点,过点A作AB∥x轴,AC∥y轴,分别交反比例函数y=![]() 的图象于点B,C,连接BC,E是BC上一点,连接并延长AE交y轴于点D,连接CD,则S△DEC﹣S△BEA=_________.
的图象于点B,C,连接BC,E是BC上一点,连接并延长AE交y轴于点D,连接CD,则S△DEC﹣S△BEA=_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∴P是菱形ABCD对角线AC上的一点,连接DP并延长DP交边AB于点E,连接BP并延长BP交边AD于点F,交CD的延长线于点G.

(1)求证:△APB≌△APD;
(2)已知DF:FA=1:2,设线段DP的长为x,线段PF的长为y.
①求y与x的函数关系式;
②当x=6时,求线段FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是![]() 的中点,CE⊥AB于点E,BD交CE于点F.
的中点,CE⊥AB于点E,BD交CE于点F.
(1)求证:CF=BF;
(2)若CD=5,AC=12,求⊙O的半径和CE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com