
【题目】为了了解某次运动会![]() 名运动员的年龄情况,从中抽查了
名运动员的年龄情况,从中抽查了![]() 名运动员的年龄,就这个问题而言,下列说法正确的是( )
名运动员的年龄,就这个问题而言,下列说法正确的是( )
A. ![]() 名运动员是总体 B. 每名运动员是个体
名运动员是总体 B. 每名运动员是个体
C. ![]() 名运动员是抽取的一个样本 D. 这种调查方式是抽样调查
名运动员是抽取的一个样本 D. 这种调查方式是抽样调查
 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),抛物线与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论

①a-b+c>0;②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在菱形 ABCD 中,∠ABC=60°,M、N 分别是边 BC,CD 上的两个动点,∠MAN=60°,AM、AN 分别交 BD 于 E、F 两点.
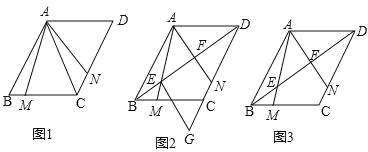
(1)如图 1,求证:CM+CN=BC;
(2)如图 2,过点 E 作 EG∥AN 交 DC 延长线于点 G,求证:EG=EA;
(3)如图 3,若 AB=1,∠AED=45°,直接写出 EF 的长.
(4)如图 3,若 AB=1,直接写出![]() BE+AE的最小值
BE+AE的最小值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣![]() x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果抛物线C1的顶点在抛物线C2上,同时,抛物线C2的顶点在抛物线C1上,那么,我们称抛物线C1与C2关联.
(1)已知两条抛物线①:y=x2+2x﹣1,②:y=﹣x2+2x+1,判断这两条抛物线是否关联,并说明理由;
(2)抛物线C1:y=![]() (x+1)2﹣2,动点P的坐标为(t,2),将抛物线C1绕点P(t,2)旋转180°得到抛物线C2,若抛物线C2与C1关联,求抛物线C2的解析式.
(x+1)2﹣2,动点P的坐标为(t,2),将抛物线C1绕点P(t,2)旋转180°得到抛物线C2,若抛物线C2与C1关联,求抛物线C2的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图某小船准备从![]() 处出发,沿北偏东
处出发,沿北偏东![]() 的方向航行,在规定的时间将一批物资运往
的方向航行,在规定的时间将一批物资运往![]() 处的货船上,后考虑这条航线可能会因退潮而使小船搁浅,决定改变航线,从
处的货船上,后考虑这条航线可能会因退潮而使小船搁浅,决定改变航线,从![]() 处出发沿正东方向航行
处出发沿正东方向航行![]() 海里到达
海里到达![]() 处,再由
处,再由![]() 处沿北偏东
处沿北偏东![]() 的方向航行到达
的方向航行到达![]() 处.
处.

(1)小船由![]() 经
经![]() 到达
到达![]() 走了多少海里(结果精确到
走了多少海里(结果精确到![]() 海里);
海里);
(2)为了按原定时间到达![]() 处的货船上,小船提速,每小时增加
处的货船上,小船提速,每小时增加![]() 海里,求小船原定的速度(结果精确到
海里,求小船原定的速度(结果精确到![]() 海里/时).
海里/时).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
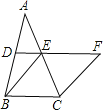
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是二次函数![]() 的部分
的部分![]() 的对应值:
的对应值:
x | … | -1 |
| 0 |
| 1 |
| 2 |
| 3 | … |
y | … | m |
| -1 |
| -2 |
| -1 |
| 2 | … |
(1)求函数解析式;
(2)当![]() 时,y的取值范围是___________;
时,y的取值范围是___________;
(3)当抛物线![]() 的顶点在直线
的顶点在直线![]() 的下方时,n的取值范围是__________.
的下方时,n的取值范围是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com