
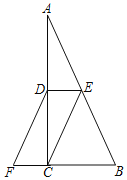
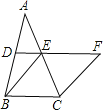
【题目】如图,在△ABC中,∠ACB=90°,点D、E分别是AC、AB的中点,点F在BC的延长线上,且∠CDF=∠A.
(1)求证:四边形DECF是平行四边形;
(2)若∠A=30°,写出图中所有与FD长度相等的线段.
【答案】(1)见解析;(2)AE=EB=BC=EC=DF
【解析】
(1)首先利用三角形中位线的性质得出DE∥BC,进而结合直角三角形的性质得出CE=![]() AB=AE,得出∠CDF=∠ACE,推出DF∥CE,再利用平行四边形的定义判定即可.
AB=AE,得出∠CDF=∠ACE,推出DF∥CE,再利用平行四边形的定义判定即可.
(2)只要证明△EBC是等边三角形即可判定;
(1)证明:∵D,E分别为AC,AB的中点,
∴DE为△ACB的中位线,
∴DE//BC.
∵CE为Rt△ACB的斜边上的中线,
∴CE=![]() AB=AE.
AB=AE.
∴∠A=∠ACE.
又∵∠CDF=∠A,
∴∠CDF=∠ACE.
∴DF//CE.
又∵DE//BC,
∴四边形DECF为平行四边形.
(2)解:图中所有与FD长度相等的线段有:AE、BE、CE、BC;理由如下:
∵∠A=30°,∠ACB=90°,
∴∠B=60°,
∵EC=EA=EB,
∴△EBC是等边三角形,
∴AE=EB=BC=EC=DF.


科目:初中数学 来源: 题型:
【题目】如图,有一个池塘,其底面是边长为10尺的正方形,一个芦苇AB生长在它的中央,高出水面部分BC为1尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B′.则这根芦苇的长度是( )

A. 10尺 B. 11尺 C. 12尺 D. 13尺
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() (
(![]() )与直线
)与直线![]() 相交于点P(2,m),与x轴交于点A.
相交于点P(2,m),与x轴交于点A.
(1)求m的值;
(2)过点P作PB⊥x轴于B,如果△PAB的面积为6,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),抛物线与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论

①a-b+c>0;②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
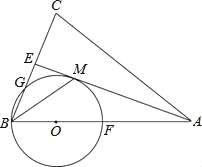
【题目】如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线 BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交 AB于点F.
(1)求证:AE为⊙O的切线.
(2)当BC=8,AC=12时,求⊙O的半径.
(3)在(2)的条件下,求线段BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=![]() 在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( )
在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( )

A. 36 B. 12 C. 6 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B(3,3)在双曲线![]() (x>0)上,点D在双曲线
(x>0)上,点D在双曲线![]() (x<0)上,点A和点C分别在x轴,y轴的正半轴上,且点A,B,C,D构成的四边形为正方形.
(x<0)上,点A和点C分别在x轴,y轴的正半轴上,且点A,B,C,D构成的四边形为正方形.
(1)求k的值;
(3)求点A的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在菱形 ABCD 中,∠ABC=60°,M、N 分别是边 BC,CD 上的两个动点,∠MAN=60°,AM、AN 分别交 BD 于 E、F 两点.
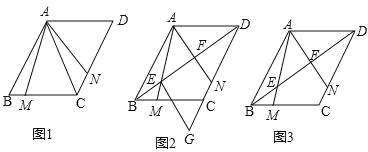
(1)如图 1,求证:CM+CN=BC;
(2)如图 2,过点 E 作 EG∥AN 交 DC 延长线于点 G,求证:EG=EA;
(3)如图 3,若 AB=1,∠AED=45°,直接写出 EF 的长.
(4)如图 3,若 AB=1,直接写出![]() BE+AE的最小值
BE+AE的最小值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com