
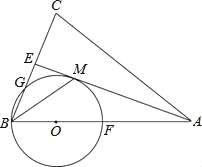
【题目】如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线 BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交 AB于点F.
(1)求证:AE为⊙O的切线.
(2)当BC=8,AC=12时,求⊙O的半径.
(3)在(2)的条件下,求线段BG的长.
【答案】(1)证明见解析;(2)3;(3)2.
【解析】试题分析:(1)连接OM.利用角平分线的性质和平行线的性质得到AE⊥OM后即可证得AE是⊙O的切线;
(2)设⊙O的半径为R,根据OM∥BE,得到△OMA∽△BEA,利用平行线的性质得到![]() ,即可解得R=3,从而求得⊙O的半径为3;
,即可解得R=3,从而求得⊙O的半径为3;
(3)过点O作OH⊥BG于点H,则BG=2BH,根据∠OME=∠MEH=∠EHO=90°,得到四边形OMEH是矩形,从而得到HE=OM=3和BH=1,证得结论BG=2BH=2.
试题解析:(1)证明:连接OM.
∵AC=AB,AE平分∠BAC,
∴AE⊥BC,CE=BE=![]() BC=4,
BC=4,
∵OB=OM,
∴∠OBM=∠OMB,
∵BM平分∠ABC,
∴∠OBM=∠CBM,
∴∠OMB=∠CBM,
∴OM∥BC
又∵AE⊥BC,
∴AE⊥OM,
∴AE是⊙O的切线;
(2)设⊙O的半径为R,
∵OM∥BE,
∴△OMA∽△BEA,
∴![]() 即
即![]() ,
,
解得R=3,
∴⊙O的半径为3;
(3)过点O作OH⊥BG于点H,则BG=2BH,
∵∠OME=∠MEH=∠EHO=90°,
∴四边形OMEH是矩形,
∴HE=OM=3,
∴BH=1,
∴BG=2BH=2.


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
【题目】下列命题中,是真命题的是( )
A. 两条直线被第三条直线所截,同位角相等B. 垂直于同一直线的两直线平行
C. 相等的角是对顶角D. 平行于同一直线的两直线平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,各地“广场舞”噪音干扰的问题倍受关注.相关人员对本地区15~65岁年龄段的市民进行了随机调查,并制作了如下相应的统计图.市民对“广场舞”噪音干扰的态度有以下五种:A.没影响 B.影响不大 C.有影响,建议做无声运动 D.影响很大,建议取缔 E.不关心这个问题
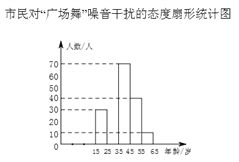
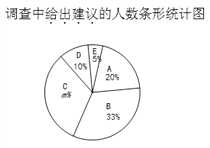
根据以上信息解答下列问题:
(1)根据统计图填空: ![]() ,A区域所对应的扇形圆心角为 度;
,A区域所对应的扇形圆心角为 度;
(2)在此次调查中,“不关心这个问题”的有25人,请问一共调查了多少人?
(3)将条形统计图补充完整;
(4)若本地共有14万市民,依据此次调查结果估计本地市民中会有多少人给出建议?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【新知理解】
如图①,点C在线段AB上,图中共有三条线段AB、AC和BC,若其中有一条线段的长度是另外一条线段长度的2倍,则称点C是线段AB的“巧点”.
线段的中点__________这条线段的“巧点”;(填“是”或“不是”).
若AB = 12cm,点C是线段AB的巧点,则AC=___________cm;
【解决问题】
(3) 如图②,已知AB=12cm.动点P从点A出发,以2cm/s的速度沿AB向点B匀速移动:点Q从点B出发,以1cm/s的速度沿BA向点A匀速移动,点P、Q同时出发,当其中一点到达终点时,运动停止,设移动的时间为t(s).当t为何值时,A、P、Q三点中其中一点恰好是另外两点为端点的线段的巧点?说明理由

![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=CD=8,过点B作EB⊥AB,交CD于点E.若DE=6,则AD的长为( ) 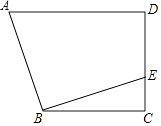
A.6
B.8
C.9
D.10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com