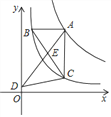
[题目]如图.点A是反比例函数y=图象上的任意一点.过点A作AB∥x轴.AC∥y轴.分别交反比例函数y=的图象于点B.C.连接BC.E是BC上一点.连接并延长AE交y轴于点D.连接CD.则S△DEC﹣S△BEA= ．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，点A是反比例函数y=图象上的任意一点，过点A作AB∥x轴，AC∥y轴，分别交反比例函数y=的图象于点B，C，连接BC，E是BC上一点，连接并延长AE交y轴于点D，连接CD，则S△DEC﹣S△BEA=_________．

【答案】

【解析】分析：设A（a，），可得B（），C（a，），进而得到AB=a，AC=，依据S△DEC﹣S△BEA=S△DAC﹣S△BCA进行计算即可．

详解：点A是反比例函数y=图象上的任意一点，可设A（a，）．

∵AB∥x轴，AC∥y轴，点B，C，在反比例函数y=的图象上，∴B（），C（a，），∴AB=a，AC=，∴S△DEC﹣S△BEA=S△DAC﹣S△BCA=××（a﹣a）=××a=．

故答案为：．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】定义：若线段AB上有一点P，当PA=PB时，则称点P为线段AB的中点。

已知数轴上A，B两点对应数分别为a和b，，P为数轴上一动点，对应数为x．

（1）a=______，b=_______；

（2）若点P为线段AB的中点，则P点对应的数为______________．若B为线段AP的中点时则P点对应的数为______________。

（3）若点A、点B同时向左运动，它们的速度都为1个单位长度/秒，与此同时点P从-16处以2个单位长度/秒向右运动。

①设运动的时间为t秒，直接用含t的式子填空

AP=____________；BP=______________。

②经过多长时间后，点A、点B、点P三点中其中一点是另外两点的中点？

查看答案和解析>>

科目：初中数学 来源： 题型：

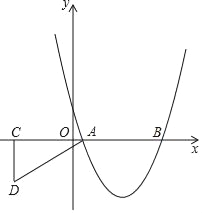
【题目】如图，抛物线y=x2+bx+c与x轴分别交于A（1，0），B（5，0）两点．

（1）求抛物线的解析式；

（2）过点C（﹣3，0）在x轴下方作x轴的垂线，再以点A为圆心、5为半径长画弧，交先前所作垂线于D，连接AD（如图），将Rt△ACD沿x轴向右平移m个单位，当点D落在抛物线上时，求m的值；

（3）在（2）的条件下，当点D第一次落在抛物线上记为点E，点P是抛物线对称轴上一点．试探究：在抛物线上是否存在点Q，使以点B、E、P、Q为顶点的四边形是平行四边形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】计算

(1)(-3)-(-2)+(-4)

(2)(-)-(-)-|-|-(-)

(3)-23÷×(-)2

(4)()×(-36)

(5)-14-×

(6)(-1)4+5÷(-)×(-6)

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知AB//CD，点C在点D的右侧，∠ABC，∠ADC的平分线交于点E(不与B，D点重合).，.

(1)若点B在点A的左侧，求∠BED的度数(用含的代数式表示).

(2)将线段BC沿DC方向平移，当点B移动到点A右侧时，请画出图形并判断的度数是否改变.若改变，请求出的度数(用含的代数式表示)；若不变，请说明理由.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知点P为∠EAF平分线上一点，PB⊥AE于B，PC⊥AF于C，点M，N分别是射线AE，AF上的点，且PM=PN．

（1）如图1，当点M在线段AB上，点N在线段AC的延长线上时，求证：BM=CN；

（2）在（1）的条件下，直接写出线段AM，AN与AC之间的数量关系；

（3）如图2，当点M在线段AB的延长线上，点N在线段AC上时，若AC：PC=2：1，且PC=4，求四边形ANPM的面积．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】随着社会的发展，通过微信朋友圈发布自己每天行走的步数已经成为一种时尚．“健身达人”小陈为了了解他的好友的运动情况．随机抽取了部分好友进行调查，把他们6月1日那天行走的情况分为四个类别：A（0～5000步）（说明：“0～5000”表示大于等于0，小于等于5000，下同），B（5001～10000步），C（10001～15000步），D（15000步以上），统计结果如图所示：