
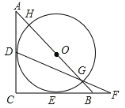
【题目】如图,△ABC是等腰直角三角形,AC=BC=2,以斜边AB上的点O为圆心的圆分别与AC、BC相切于点D、E,与AB分别相交于点G、H,且DG的延长线与CB的延长线交于点F,分析下列四个结论:①HG=2;②BG=BF;③AH=BG=![]() ;④CF=
;④CF= ![]() .其中正确的结论个数有( )
.其中正确的结论个数有( )
A.1个B.2个C.3个D.4个
【答案】D
【解析】
如右图所示,连接OD、OE,根据切线的性质得到∠ODC=∠OEC=90°,OE=OD,据等腰直角三角形的性质得到∠C=90°,∠A=45°,得到四边形DCEO是正方形,求得OD=AD=![]() AC=1,于是得到HG=2OD=2;故①正确;求得∠EOB=45°,得到∠ODG=135°,得到∠OGD=∠ODG=22.5°,根据等腰三角形的性质得到BG=BF,故②正确;根据角平分线的判定定理得到O在∠ACB的角平分线上,根据等腰三角形的性质得到O是AB中点,求得AD=CD=OD=OE=1,得到OG=1,根据勾股定理得到AB=
AC=1,于是得到HG=2OD=2;故①正确;求得∠EOB=45°,得到∠ODG=135°,得到∠OGD=∠ODG=22.5°,根据等腰三角形的性质得到BG=BF,故②正确;根据角平分线的判定定理得到O在∠ACB的角平分线上,根据等腰三角形的性质得到O是AB中点,求得AD=CD=OD=OE=1,得到OG=1,根据勾股定理得到AB=
![]() AC=
AC=![]() ,于是得到AH=BG=
,于是得到AH=BG=![]() ,故③正确;CF=2+BF=
,故③正确;CF=2+BF=![]() .故④正确.
.故④正确.
如右图所示,连接OD、OE,
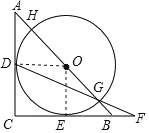
∵⊙O与AC、BC切于点D. E,
∴∠ODC=∠OEC=90°,OE=OD,
又∵△ABC是等腰直角三角形,
∴∠C=90°,∠A=45°,
∴四边形DCEO是正方形,
∴OD∥BC,OE=OD,OD⊥AC,
△ADO是等腰直角三角形,
∴OD=AD=![]() AC=1,
AC=1,
∴HG=2OD=2;故①正确;
∵AC=BC,∴∠A=∠ABC=45°,
∴∠EOB=45°,
∴∠ODG=135°,
∵OD=OG,
∴∠OGD=∠ODG=22.5°,
∴∠BGF=22.5°,
∵∠BGF+∠F=∠ABC=45°,
∴∠F=22.5°,
∴BG=BF,故②正确;
∵OE=OD,
∴O在∠ACB的角平分线上,
∴O是AB中点,
∴AD=CD,
又∵AC=2,
∴AD=CD=OD=OE=1,
∴OG=1,
又∵AB![]() AC=
AC=![]() ,
,
∴OB=![]() ,
,
∴BG=OBOG=![]() ,
,
同理AH=BG=![]() ,故③正确;
,故③正确;
∴CF=2+BF=![]() .故④正确。
.故④正确。
故选D.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①ac<0,②b﹣2a<0,③b2﹣4ac<0,④a﹣b+c<0,正确的是( )
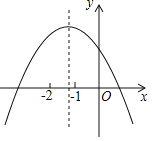
A.①②B.①④C.②③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k<0;②a>0;③当x<3时,y1<y2;④当y1>0且y2>0时,﹣a<x<4.其中正确的个数是( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=﹣![]() x+
x+![]() 与x轴交于点A,与y轴交于点B;抛物线y=ax2+bx+
与x轴交于点A,与y轴交于点B;抛物线y=ax2+bx+![]() (a≠0)过A,B两点,与x轴交于另一点C(﹣1,0),抛物线的顶点为D.
(a≠0)过A,B两点,与x轴交于另一点C(﹣1,0),抛物线的顶点为D.
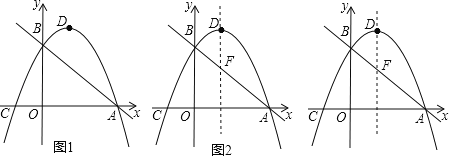
(1)求出A,B两点的坐标;
(2)求抛物线的解析式及顶点D的坐标;
(3)在直线AB上方的抛物线上有一动点E,求出点E到直线AB的距离的最大值;
(4)如图2,直线AB与抛物线的对称轴相交于点F,点P在坐标轴上,且点P到直线BD,DF的距离相等,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
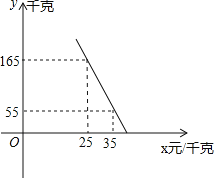
【题目】水果店王阿姨到水果批发市场打算购进一种水果销售,经过还价,实际价格每千克20元。王阿姨准备购进这种水果销售,若这种水果的销售量y(千克)与销售单价x(元/千克)满足如图所示的一次函数关系.
(1)求y与x之间的函数关系式;
(2)请你帮王阿姨拿个主意,将这种水果的销售单价定为多少时,能获得最大利润?最大利润是多少?(利润=销售收入-进货金额)
查看答案和解析>>
科目:初中数学 来源: 题型:
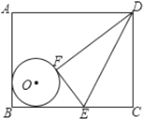
【题目】如图,⊙O在矩形ABCD内,且与AB、BC边都相切,E是BC上一点,将△DCE沿DE对折,点C的对称点F恰好落在⊙O上,已知AB=20,BC=25,CE=10,则⊙O的半径为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
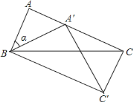
【题目】如图,在△ABC中,∠A=80°,AC=BC,以点B为旋转中心把△ABC按顺时针旋转α度,得到△A′BC′,点A′恰好落在AC上,连接CC′,则∠ACC′=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直角△ABC,∠C=90°,BC=3,AC=4.⊙C的半径长为1,已知点P是△ABC边上一动点(可以与顶点重合)
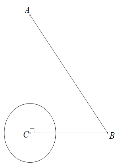
(1)若点P到⊙C的切线长为![]() ,则AP的长度为 ;
,则AP的长度为 ;
(2)若点P到⊙C的切线长为m,求点P的位置有几个?(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC=a,BD=b,且AC丄BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2…,如此进行下去,得到四边形AnBnnDn.下列结论正确的有( )
①四边形A2B2C2D2是矩形;
②四边形A4B4C4D4是菱形;
③四边形A5B5C5D5的周长是![]()
④四边形AnBnnDn的面积是![]() .
.

A.①②B.②③C.②③④D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com