
【题目】如图,⊙O在矩形ABCD内,且与AB、BC边都相切,E是BC上一点,将△DCE沿DE对折,点C的对称点F恰好落在⊙O上,已知AB=20,BC=25,CE=10,则⊙O的半径为______.
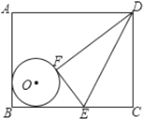
【答案】5
【解析】
过点F作AD,BC的垂线GH,过O作MN∥BC交AB于M,GH于N,易证△DGF∽△FHE,利用相似三角形的性质即可求出DG=HC=16,GF=12,FH=8,设圆O的半径为r,在直角三角形FON中,利用勾股定理可得关于r的方程,解方程求出r的值即可.
过点F作AD,BC的垂线GH,过O作MN∥BC交AB于M,GH于N,
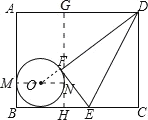
∵四边形ABCD是矩形,
∴∠C=90°,
∵将△DCE沿DE对折,点C的对称点F恰好落在O上,
∴∠DFE=90°,
∴∠GFD+∠HFE=90°,
∵∠GFD+∠GDF=90°,
∴∠GDF=∠HFE,
∴△DGF∽△FHE,
∴![]() ,
,
∵AB=20,BC=25,CE=10,
∴DG=HC=16,GF=12,FH=8,
设圆O的半径为r,
在直角三角形FON中, ![]() ,
,
解得:r=5,
故答案为:5.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+2的图象交x轴于点A(﹣1,0),点B(4,0)两点,交y轴于点C.动点M从点A出发,以每秒2个单位长度的速度沿AB方向运动,过点M作MN⊥x轴交直线BC于点N,交抛物线于点D,连接AC,设运动的时间为t秒.
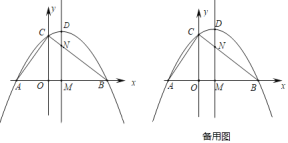
(1)求二次函数y=ax2+bx+2的表达式;
(2)连接BD,当t=![]() 时,求△DNB的面积;
时,求△DNB的面积;
(3)在直线MN上存在一点P,当△PBC是以∠BPC为直角的等腰直角三角形时,求此时点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学准各去湿地公园开展社会实践活动,学校给出A:十八弯,B:长广溪,C:九里河,D:贡湖湾,共四个目的地.为了解学生最喜欢哪一个目的地,随机抽取了部分学生进行调査,并将调査结果绘制了如下两幅不完整的统计图.请回答下列问题:
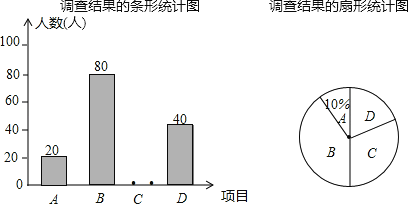
(1)这次被调査的学生共有 人.
(2)请你将条形统计图补充完整.
(3)扇形统计图中D项目对立的扇形的圆心角度数是 °.
(4)已知该校学生2400人,请根据调査结果估计该校最喜欢去长广溪湿地公园的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
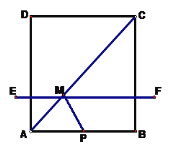
【题目】如图,正方形ABCD的边长AB是方程![]() 的一个根,动点P从A至B以3cm/s的速度移动,动直线EF从与AB重合的位置开始向上以1cm/s速度移动(EF∥AB),EF交AD、AC、BC于E、M、F。设运动时间为t秒.
的一个根,动点P从A至B以3cm/s的速度移动,动直线EF从与AB重合的位置开始向上以1cm/s速度移动(EF∥AB),EF交AD、AC、BC于E、M、F。设运动时间为t秒.
(1)当t=1时,四边形MFBP的面积为 .用t表示△APM的面积为 .
(2)在某一时刻t,使△APM与四边形MFBP的面积相等,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,AC=BC=2,以斜边AB上的点O为圆心的圆分别与AC、BC相切于点D、E,与AB分别相交于点G、H,且DG的延长线与CB的延长线交于点F,分析下列四个结论:①HG=2;②BG=BF;③AH=BG=![]() ;④CF=
;④CF= ![]() .其中正确的结论个数有( )
.其中正确的结论个数有( )
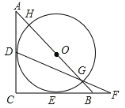
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
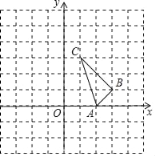
【题目】在平面直角坐标系中,已知A(2,0)、B(3,1)、C(1,3).
(1)画出△ABC沿x轴负方向平移2个单位后得到的△A1B1C1,并写出B1的坐标 ;
(2)以A1点为旋转中心,将△A1B1C1逆时针方向旋转90°得△A1B2C2,画出△A1B2C2,并写出C2的坐标 ;
(3)直接写出过B、B1、C2三点的圆的圆心坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,折叠矩形ABCD,使点B落在对角线AC上的点F处,若BC=8,AB=6,则线段CE的长度是( )

A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家限购以来,二手房和新楼盘的成交量迅速下降.据统计,某市限购前某季度二手房和新楼盘成交量为9500套;限购后,同一季度二手房和新楼盘的成交量共4425套.其中二手房成交量比限购前减少55%,新楼盘成交量比限购前减少52%.
(1)问限购后二手房和新楼盘各成交多少套?
(2)在成交量下跌的同时,房价也大幅跳水.某楼盘限购前均价为12000元/m2,限购后,房价经过二次下调后均价为9720元/m2![]() ,求平均每次下调的百分率.
,求平均每次下调的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解方程。
(1)4(x-3) ![]() =36
=36
(2)x2-4x+1=0.
(3)![]() -7x+6=0
-7x+6=0
(4)![]()
(5)(y-1)2+2y(1-y)=0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com