
ЁОЬтФПЁПФГжабЇзМИїШЅЪЊЕиЙЋдАПЊеЙЩчЛсЪЕМљЛюЖЏЃЌбЇаЃИјГіAЃКЪЎАЫЭфЃЌBЃКГЄЙуЯЊЃЌCЃКОХРяКгЃЌDЃКЙБКўЭхЃЌЙВЫФИіФПЕФЕиЃЎЮЊСЫНтбЇЩњзюЯВЛЖФФвЛИіФПЕФЕиЃЌЫцЛњГщШЁСЫВПЗжбЇЩњНјааЕїЫЃЌВЂНЋЕїЫНсЙћЛцжЦСЫШчЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЎЧыЛиД№ЯТСаЮЪЬтЃК
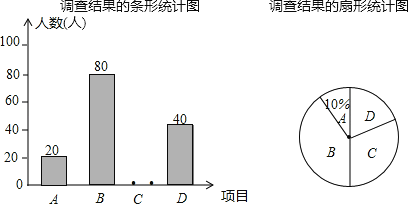
ЃЈ1ЃЉетДЮБЛЕїЫЕФбЇЩњЙВгаЁЁ ШЫЃЎ
ЃЈ2ЃЉЧыФуНЋЬѕаЮЭГМЦЭМВЙГфЭъећЃЎ
ЃЈ3ЃЉЩШаЮЭГМЦЭМжаDЯюФПЖдСЂЕФЩШаЮЕФдВаФНЧЖШЪ§ЪЧЁЁ ЁуЃЎ
ЃЈ4ЃЉвбжЊИУаЃбЇЩњ2400ШЫЃЌЧыИљОнЕїЫНсЙћЙРМЦИУаЃзюЯВЛЖШЅГЄЙуЯЊЪЊЕиЙЋдАЕФбЇЩњШЫЪ§ЃЎ
ЁОД№АИЁПЃЈ1ЃЉ200ЃЛЃЈ2ЃЉВЙШЋЭМаЮМћНтЮіЃЛЃЈ3ЃЉ72ЃЛЃЈ4ЃЉ960ШЫЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгУAзщЕФШЫЪ§Г§вдАйЗжБШМДПЩЧѓНт
ЃЈ2ЃЉгУзмШЫЪ§МѕШЅЦфЫћМИзщЕФШЫЪ§МДПЩЧѓНт
ЃЈ3ЃЉгУ360ЁуГЫвдDзщЕФеМБШМДПЩЧѓНт
ЃЈ4ЃЉгУзмШЫЪ§ГЫвдBзщЕФеМБШМДПЩЧѓНт
ЃЈ1ЃЉетДЮЕїВщЕФбЇЩњзмШЫЪ§ЮЊ20ЁТ10%ЃН200ЃЈШЫЃЉЃЌ
ЙЪД№АИЮЊЃК200ЃЛ
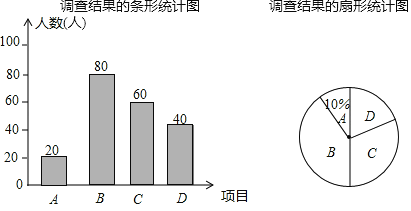
ЃЈ2ЃЉCЯюФПШЫЪ§ЮЊ200ЉЃЈ20+80+40ЃЉЃН60ЃЈШЫЃЉЃЌ
ВЙШЋЭМаЮШчЯТЃК
ЃЈ3ЃЉЩШаЮЭГМЦЭМжаDЯюФПЖдгІЕФЩШаЮЕФдВаФНЧЖШЪ§ЪЧ360ЁуЁС![]() ЃН72ЁуЃЌ
ЃН72ЁуЃЌ
ЙЪД№АИЮЊЃК72ЃЛ
ЃЈ4ЃЉИљОнЕїЫНсЙћЙРМЦИУаЃзюЯВЛЖШЅГЄЙуЯЊЪЊЕиЙЋдАЕФбЇЩњШЫЪ§ЮЊ2400ЁС![]() ЃН960ЃЈШЫЃЉЃЎ
ЃН960ЃЈШЫЃЉЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
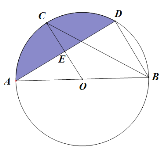
ЁОЬтФПЁПШчЭМЃЌвбжЊABЪЧЁбOЕФжБОЖЃЌCЃЌDЪЧЁбOЩЯЕФЕуЃЌOCЁЮBDЃЌНЛADгкЕуEЃЌСЌНсBCЃЎ
ЃЈ1ЃЉЧѓжЄЃКAE=EDЃЛ
ЃЈ2ЃЉШєAB=8ЃЌЁЯCBD=30ЁуЃЌЧѓЭМжавѕгАВПЗжЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЁїABCЕФШ§ИіЖЅЕузјБъЗжБ№ЪЧAЃЈ1ЃЌ1ЃЉЃЌBЃЈ4ЃЌ1ЃЉЃЌCЃЈ3ЃЌ3ЃЉЃЎ
ЃЈ1ЃЉНЋЁїABCЯђЯТЦНвЦ5ИіЕЅЮЛКѓЕУЕНЁїA1B1C1ЃЌЧыЛГіЁїA1B1C1ЃЛ
ЃЈ2ЃЉНЋЁїABCШЦдЕуOФцЪБеыа§зЊ90ЁуКѓЕУЕНЁїA2B2C2ЃЌЧыЛГіЁїA2B2C2ЃЛ
ЃЈ3ЃЉХаЖЯвдOЃЌA1ЃЌBЮЊЖЅЕуЕФШ§НЧаЮЕФаЮзДЃЎЃЈЮоаыЫЕУїРэгЩЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФЗНГЬ![]()
ЃЈ1ЃЉЧѓжЄЃКВЛТлkШЁЪВУДЪЕЪ§жЕЃЌетИіЗНГЬзмгаЪЕЪ§ИљЃЛ
ЃЈ2ЃЉШєЕШбќШ§НЧаЮABCЕФвЛБпГЄЮЊ![]() ЃЌСэСНБпЕФГЄbЁЂcЧЁКУЪЧетИіЗНГЬЕФСНИіИљЃЌЧѓЁїABCЕФжмГЄЃЎ
ЃЌСэСНБпЕФГЄbЁЂcЧЁКУЪЧетИіЗНГЬЕФСНИіИљЃЌЧѓЁїABCЕФжмГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛДЮКЏЪ§y1ЃНkx+bгыy2ЃНx+aЕФЭМЯѓШчЭМЫљЪОЃЌдђЯТСаНсТлЃКЂйkЃМ0ЃЛЂкaЃО0ЃЛЂлЕБxЃМ3ЪБЃЌy1ЃМy2ЃЛЂмЕБy1ЃО0Чвy2ЃО0ЪБЃЌЉaЃМxЃМ4ЃЎЦфжае§ШЗЕФИіЪ§ЪЧЃЈЁЁЁЁЃЉ

A.1ИіB.2ИіC.3ИіD.4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌЯШНЋХзЮяЯпyЃН2x2Љ4xЙигкyжсзїжсЖдГЦБфЛЛЃЌдйНЋЫљЕУЕФХзЮяЯпЃЌШЦЫќЕФЖЅЕуа§зЊ180ЁуЃЌФЧУДОСНДЮБфЛЛКѓЫљЕУЕФаТХзЮяЯпЕФКЏЪ§БэДяЪНЮЊЃЈЁЁЁЁЃЉ
A.yЃНЉ2x![]() Љ4xB.yЃНЉ2x
Љ4xB.yЃНЉ2x![]() +4x
+4x
C.yЃНЉ2x![]() Љ4xЉ4D.yЃНЉ2x
Љ4xЉ4D.yЃНЉ2x![]() +4x+4
+4x+4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯпy=Љ![]() x+
x+![]() гыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуBЃЛХзЮяЯпy=ax2+bx+
гыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуBЃЛХзЮяЯпy=ax2+bx+![]() ЃЈaЁй0ЃЉЙ§AЃЌBСНЕуЃЌгыxжсНЛгкСэвЛЕуCЃЈЉ1ЃЌ0ЃЉЃЌХзЮяЯпЕФЖЅЕуЮЊDЃЎ
ЃЈaЁй0ЃЉЙ§AЃЌBСНЕуЃЌгыxжсНЛгкСэвЛЕуCЃЈЉ1ЃЌ0ЃЉЃЌХзЮяЯпЕФЖЅЕуЮЊDЃЎ
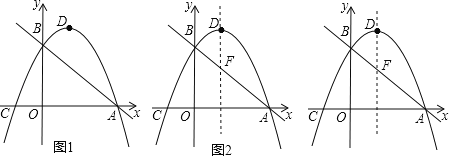
ЃЈ1ЃЉЧѓГіAЃЌBСНЕуЕФзјБъЃЛ
ЃЈ2ЃЉЧѓХзЮяЯпЕФНтЮіЪНМАЖЅЕуDЕФзјБъЃЛ
ЃЈ3ЃЉдкжБЯпABЩЯЗНЕФХзЮяЯпЩЯгавЛЖЏЕуEЃЌЧѓГіЕуEЕНжБЯпABЕФОрРыЕФзюДѓжЕЃЛ
ЃЈ4ЃЉШчЭМ2ЃЌжБЯпABгыХзЮяЯпЕФЖдГЦжсЯрНЛгкЕуFЃЌЕуPдкзјБъжсЩЯЃЌЧвЕуPЕНжБЯпBDЃЌDFЕФОрРыЯрЕШЃЌЧыжБНгаДГіЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
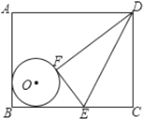
ЁОЬтФПЁПШчЭМЃЌЁбOдкОиаЮABCDФкЃЌЧвгыABЁЂBCБпЖМЯрЧаЃЌEЪЧBCЩЯвЛЕуЃЌНЋЁїDCEбиDEЖделЃЌЕуCЕФЖдГЦЕуFЧЁКУТфдкЁбOЩЯЃЌвбжЊAB=20ЃЌBC=25ЃЌCE=10ЃЌдђЁбOЕФАыОЖЮЊ______.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊжБЯпlЃКyЃНЉ1КЭХзЮяЯпLЃКyЃНax2+bx+cЃЈaЁй0ЃЉЃЌХзЮяЯпLЕФЖЅЕуЮЊдЕуЃЌЧвОЙ§ЕуA(2![]() ,
,![]() )ЃЌжБЯпyЃНkx+1гыyжсНЛгкЕуFЃЌгыХзЮяЯпLНЛгкЕуBЃЈx1ЃЌy1ЃЉЃЌCЃЈx2ЃЌy2ЃЉЃЌЧвx1ЃМx2ЃЎ
)ЃЌжБЯпyЃНkx+1гыyжсНЛгкЕуFЃЌгыХзЮяЯпLНЛгкЕуBЃЈx1ЃЌy1ЃЉЃЌCЃЈx2ЃЌy2ЃЉЃЌЧвx1ЃМx2ЃЎ
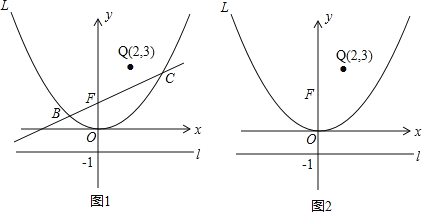
ЃЈ1ЃЉЧѓХзЮяЯпLЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуPЪЧХзЮяЯпLЩЯвЛЖЏЕуЃЎ
ЂйвдЕуPЮЊдВаФЃЌPFЮЊАыОЖзїЁбPЃЌЪдХаЖЯЁбPгыжБЯпlЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЂкШєЕуQЃЈ2ЃЌ3ЃЉЃЌЕБ|PQЉPF|ЕФжЕзюаЁЪБЃЌЧѓЕуPЕФзјБъЃЛ
ЃЈ3ЃЉЧѓжЄЃКЮоТлkЮЊКЮжЕЃЌжБЯпlзмЪЧгывдBCЮЊжБОЖЕФдВЯрЧаЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com