
����Ŀ�����Ǹ������¶��壺˳����������һ���ı��θ����е����õ��ı��ν��е��ı��Σ�
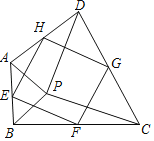
��1����ͼ����P���ı���ABCD��һ�㣬������PA��PB��PC��PD����APB����CPD����E��F��G��H�ֱ�Ϊ��AB��BC��CD��DA���е㣬�����е��ı���EFGH����״����֤����IJ��룻
��2�����ı䣨1���е�������ʹ��APB����CPD��90���������������䣬ֱ��д���е��ı���EFGH����״������֤������
���𰸡���1���ı���EFGH�����Σ����ɼ���������2���ı���EFGH�������Σ����ɼ�����
��������
��1������AC��BD����PA��PB��PC��PD����APB����CPD��֤��APC�ա�BPD��SAS����
�ʿɵõ�AC��BD�������������ε���λ�߿ɵ�EF��![]() AC��FG��
AC��FG��![]() BD��EH��
BD��EH��![]() BD��GH��
BD��GH��![]() AC����֤EF��FG��GH��EH�����ı���EFGH�����Σ�
AC����֤EF��FG��GH��EH�����ı���EFGH�����Σ�
��2����AC��BD����ΪO��AC��PD���ڵ�M��AC��EH���ڵ�N��
���á�APC�ա�BPD�����ԡ�ACP����BDP���ٸ��ݡ�CPD��90���ʡ�PDC+��PCD��90��
�á�ODC+��OCD��90��������COD��90������AC��BD����������λ�ߵ����ʡ�EHG����ENO����BOC����DOC��90�������ɵõ��ı���EFGH�������Σ�
��1���ı���EFGH�����Σ�
��ͼ������AC��BD��
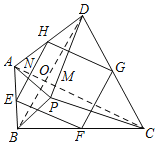
�ߡ�APB����CPD��
���APB+��APD����CPD+��APD������APC����BPD��
�ڡ�APC�͡�BPD�У�
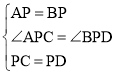 ��
��
���APC�ա�BPD��SAS����
��AC��BD��
�ߵ�E��F��G�ֱ�ΪAB��BC��CD���е㣬
��EF��![]() AC��FG��
AC��FG��![]() BD��EH��
BD��EH��![]() BD��GH��
BD��GH��![]() AC��
AC��
��EF��FG��GH��EH��
���ı���EFGH�����Σ�
��2���ı���EFGH�������Σ�
��AC��BD����ΪO��AC��PD���ڵ�M��AC��EH���ڵ�N��
�ߡ�APC�ա�BPD��
���ACP����BDP��
�ߡ�CPD��90��
���PDC+��PCD��90��
���ODC+��OCD��90��
���COD��90��
��AC��BD
��EH��BD��AC��HG��
���EHG����ENO����BOC����DOC��90����
���ı���EFGH�����Σ�
���ı���EFGH�������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�У�AB=BC=5��tan��ABC=![]() ��
��
��1�����AC�ij���
��2�����BC�Ĵ�ֱƽ�������AB�Ľ���ΪD����![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ������ ��
A�����������ݵķ���![]() ���������ݵķ���
���������ݵķ���![]() ����������ݱ��������ݴ�
����������ݱ��������ݴ�
B����1��2��3��4��5���������ȡһ��������ż���Ŀ����ԱȽϴ�
C������3��5��4��1����2�������3
D����ij����Ϸ����н�����30%����μ����ֻ10�α���3���н�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��OAB����ƽ��ֱ������ϵ�У���A������Ϊ��0��4������B������Ϊ��3��0������P��Rt��OAB����Բ��Բ�ģ���Rt��OAB��y���������������������ʹ��������������x���غϣ���һ�ι�����Բ��ΪP1���ڶ��ι�����Բ��ΪP2�����ι��ɣ���2019�ι�����Rt��OAB����Բ��Բ��P2019�������ǣ�������
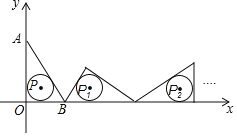
A.��673��1��B.��674��1��C.��8076��1��D.��8077��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У���ֱ�ߺ�Բ������BAD��ƽ����AG��BC�ڵ�E����BF=12��AB=10����AE�ij�Ϊ�� ��

A��16 B��15 C��14 D��13
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
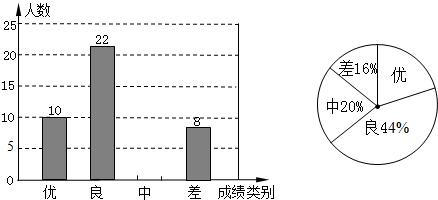
����Ŀ��Ϊ�������꼶ѧ����ѧϰ�ɼ�״������Ӧ�Լ����������п����ý�ѧ������ij��ѧ��ȡ�˲��ֲμӿ��Ե�ѧ���ijɼ���Ϊ�������������Ƴ�������������������ͳ��ͼ�������ͼ���ṩ����Ϣ����������⣺
��1������ѧ�ɼ����Ϊ���С���������
��2���������ͼ�У����š���ռ�İٷֱȣ���������ͳ��ͼ����������
��3����У���꼶����1000�˲μ�����ο��ԣ�������У���꼶���ж�����ѧ������ѧ�ɼ��ﵽ���㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�D��E�ֱ���AB��AC���е㣬BE=2DE���ӳ�DE����F��ʹ��EF=BE������CF��
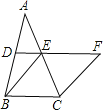
��1����֤���ı���BCFE�����Σ�
��2����CE=4����BCF=120����������BCFE�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
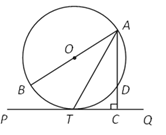
����Ŀ����ͼ��![]() Ϊ��O��ֱ���� D��T��Բ�ϵ����㣬��ATƽ�֡�BAD������T��AD�ӳ��ߵĴ���PQ������ΪC��
Ϊ��O��ֱ���� D��T��Բ�ϵ����㣬��ATƽ�֡�BAD������T��AD�ӳ��ߵĴ���PQ������ΪC��
��1����֤��PQ�ǡ�O�����ߣ�
��2������O�İ뾶Ϊ2��![]() ������AD�ij�.
������AD�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����꼶��ѧ�ڣ�����̽���ˡ����������������״�İ�װֽ�С����������Ǽ���������ѧ֪ʶ����������������������״�İ�װֽ�С��г���������.��ͼ1��һ��߳�Ϊ60cm �������α���Ƭ��������������������ͼ2��һ�����������.
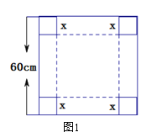
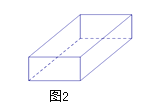

��1�����Ҫ����һ��û�иǵij�������ӣ������ڱ���Ƭ���ĸ����Ͻ�ȥ�ĸ���ͬ��С�����Σ��߳�Ϊxcm, Ȼ����ı��ۺ�����.
�������ɵĺ��ӵ����ycm2���ȥС�����α߳�xcm֮��ĺ�����ϵʽ��
�ڵ����ɵĺ��ӵĵ����Ϊ900cm2ʱ������ú��ӵ��ݻ�.
��2�����Ҫ����һ���иǵij�������ӣ�����������Ҫ��ͬʱ������������������
�ٱ����ڱ���Ƭ���ĸ����ϸ���ȥһ���ı��Σ����ಿ�ֲ��ܲýأ���
���ۺϺ���Ƭ����϶���ֲ��ص���Χ�ɸ����棬���㻭��������������������һ�ֲݰ�(����˵����������ݣ����������Ϊ800cm2ʱ���ú��ӵĸ�.)
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com