
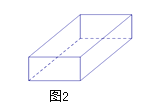
【题目】七年级上学期,我们探究了“设计制作长方体形状的包装纸盒”,今天我们继续运用所学知识,解决“设计制作长方体形状的包装纸盒”中常见的问题.如图1是一块边长为60cm 的正方形薄铁片,现在用它来制作成如图2的一个长方体盒子.
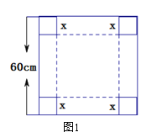

(1)如果要做成一个没有盖的长方体盒子,可先在薄铁片的四个角上截去四个相同的小正方形,边长为xcm, 然后把四边折合起来.
①求做成的盒子底面积ycm2与截去小正方形边长xcm之间的函数关系式;
②当做成的盒子的底面积为900cm2时,试求该盒子的容积.
(2)如果要做成一个有盖的长方体盒子,其制作方案要求同时符合下列两个条件:
①必须在薄铁片的四个角上各截去一个四边形(其余部分不能裁截);
②折合后薄铁片既无空隙、又不重叠地围成各盒面,请你画出符合上述制作方案的一种草案(不必说明画法与根据),并求当底面积为800cm2时,该盒子的高.)
【答案】(1)![]() ,13500cm3;(2)答案见解析,10cm.
,13500cm3;(2)答案见解析,10cm.
【解析】
(1)①可根据图中给出的信息,先表示出盒子的正方形底面的边长,然后根据正方形的面积公式即可得出x,y的函数关系式;
②可将底面积代入①的式子中,求出高,然后根据底面积×高=容积,即可得出容积是多少;
(2)只要符合要求的图形都可以,求法同(1).
解:(1)①由题意可得![]() ;
;
②当y=900时,![]() ,解得x=15,x=45(不合题意舍去),
,解得x=15,x=45(不合题意舍去),
因此盒子的容积应该是900×15=13500(立方厘米).
答:该盒子的容积是13500立方厘米.
(2)如图:
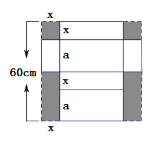
图中阴影部分为裁剪部分.
列方程得:![]() ,
,
解这个方程得:x=10或x=50(不符合题意,舍去).
∴盒子的高为10cm.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.
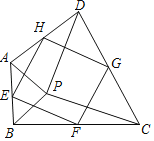
(1)如图,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(2)若改变(1)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状(不必证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】爱好数学的甲、乙两个同学做了一个数字游戏:拿出三张正面写有数字﹣1,0,1且背面完全相同的卡片,将这三张卡片背面朝上洗匀后,甲先随机抽取一张,将所得数字作为p的值,然后将卡片放回并洗匀,乙再从这三张卡片中随机抽取一张,将所得数字作为q值,两次结果记为![]() .
.
(1)请你帮他们用树状图或列表法表示![]() 所有可能出现的结果;
所有可能出现的结果;
(2)求满足关于x的方程![]() 没有实数根的概率.
没有实数根的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,某校举办了学生“国学经典大赛”.比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式为“单人组”和“双人组”.小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少?请用画树状图或列表的方法进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新华商场为迎接家电下乡活动销售某种冰箱,每台进价为2500元,市场调研表明;当销售价定为2900元时,平均每天能售出8台;而当销售价每降低50元时,平均每天就能多售出4台,商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
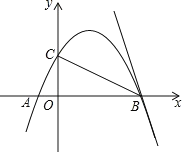
【题目】如图,抛物线y=ax2+bx+2经过点A(1,0),B(4,0),交y轴于点C;
(1)求抛物线的解析式(用一般式表示);
(2)点D为y轴右侧抛物线上一点,是否存在点D使S△ABC=![]() S△ABD?若存在,请求出点D坐标;若不存在,请说明理由;
S△ABD?若存在,请求出点D坐标;若不存在,请说明理由;
(3)将直线BC绕点B顺时针旋转45°,与抛物线交于另一点E,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,B(2m,0),C(3m,0)是平面直角坐标系中两点,其中m为常数,且m>0,E(0,n)为y轴上一动点,以BC为边在x轴上方作矩形ABCD,使AB=2BC,画射线OA,把△ADC绕点C逆时针旋转90°得△A′D′C′,连接ED′,抛物线![]() (
(![]() )过E,A′两点.
)过E,A′两点.

(1)填空:∠AOB= °,用m表示点A′的坐标:A′( , );
(2)当抛物线的顶点为A′,抛物线与线段AB交于点P,且![]() 时,△D′OE与△ABC是否相似?说明理由;
时,△D′OE与△ABC是否相似?说明理由;
(3)若E与原点O重合,抛物线与射线OA的另一个交点为点M,过M作MN⊥y轴,垂足为N:
①求a,b,m满足的关系式;
②当m为定值,抛物线与四边形ABCD有公共点,线段MN的最大值为10,请你探究a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com