
【题目】已知在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为射线
为射线![]() 上一点(与点
上一点(与点![]() 不重合),过点
不重合),过点![]() 作
作![]() 于点
于点![]() ,且
,且![]() (点
(点![]() 与点
与点![]() 在射线
在射线![]() 同侧),连接
同侧),连接![]() ,
,![]() .
.
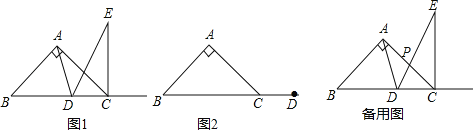
(1)如图1,当点![]() 在线段
在线段![]() 上时,请直接写出
上时,请直接写出![]() 的度数.
的度数.
(2)当点![]() 在线段
在线段![]() 的延长线上时,依题意在图2中补全图形并判断(1)中结论是否成立?若成立,请证明;若不成立,请说明理由.
的延长线上时,依题意在图2中补全图形并判断(1)中结论是否成立?若成立,请证明;若不成立,请说明理由.
(3)在(1)的条件下,![]() 与
与![]() 相交于点
相交于点![]() ,若
,若![]() ,直接写出
,直接写出![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)补全图形,如图所示,见解析;结论成立.证明见解析;(3)
;(2)补全图形,如图所示,见解析;结论成立.证明见解析;(3)![]() 的最大值为1.
的最大值为1.
【解析】
(1)先判断出![]() ,进而得出
,进而得出![]() ,即可判断出
,即可判断出![]() 是等腰直角三角形;
是等腰直角三角形;
(2)直接根据题意画出图形,同(1)的方法即可得出结论;
(3)先判断出PC最大,即可得出AP最小,利用点到直线的距离最小,得出![]() 时,AP最小,最后利用等腰直角三角形的性质即可得出结论.
时,AP最小,最后利用等腰直角三角形的性质即可得出结论.
(1)如图1,
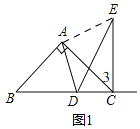
连接![]() ,
,
∵在![]() 中,
中,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() 是等腰直角三角形.
是等腰直角三角形.
∴![]() .
.
(2)补全图形,如图2所示,
结论成立.
证明:
如图,连接![]() ,
,
∵在![]() 中,
中,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() 是等腰直角三角形.
是等腰直角三角形.
∴![]() .
.
(3)由(1)知,![]() 是等腰直角三角形,
是等腰直角三角形,
∵![]() ,
,
∴![]() ,
,
当![]() 最小时,
最小时,![]() 最大,
最大,
即:![]() 时,
时,![]() 最小,
最小,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() .
.
即:![]() 的最大值为1.
的最大值为1.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,点D在AB上,以AD为直径的⊙O与BC相
交于点E,且AE平分∠BAC.
(1)求证:BC是⊙O的切线;
(2)若∠EAB=30°,OD=3,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
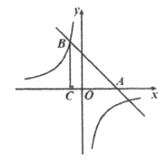
【题目】如图,在平面直角坐标系xOy中,直线![]() 与x轴交于点A,与双曲线
与x轴交于点A,与双曲线![]() 的一个交点为B(-1,4).
的一个交点为B(-1,4).
(1)求直线与双曲线的表达式;
(2)过点B作BC⊥x轴于点C,若点P在双曲线![]() 上,且△PAC的面积为4,求点P的坐标.
上,且△PAC的面积为4,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
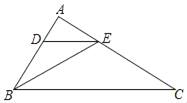
【题目】如图,在△ABC中,点D、E分别在边AB、AC上,AE2=ADAB,∠ABE=∠ACB.
(1)求证:DE∥BC;
(2)如果S△ADE:S四边形DBCE=1:8,求S△ADE:S△BDE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,点P为AD上一个动点,以PB 为对称轴将△APB折叠得到△EPB,点A的对称点为点E,射线BE交矩形ABCD的边于点 F,若AB=4,AD=6,当点F为矩形ABCD边的中点时,AP的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着生活质量的提高,人们健康意识逐渐增强,安装净水设备的百姓家庭越来越多.某厂家从去年开始投入生产净水器,生产净水器的总量y(台)与今年的生产天数x(天)的关系如图所示.今年生产90天后,厂家改进了技术,平均每天的生产数量达到30台.
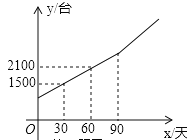
(1)求y与x之间的函数表达式;
(2)已知该厂家去年平均每天的生产数量与今年前90天平均每天的生产数量相同,求厂家去年生产的天数;
(3)如果厂家制定总量不少于6000台的生产计划,那么在改进技术后,至少还要多少天完成生产计划?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要求在下列问题中仅用无刻度的直尺作图.如图,在下列10×12的网格中, 横、纵坐标均为整数的点叫做格点.例如正方形ABCD的顶点A(0,7),C(5,2)都是格点.
(1)找一个格点M, 连接AM交边CD于F,使DF=FC,画出图形写出点M的坐标为 ;
(2)找一个格点N, 连接ON交边BC于E,使BE=![]() BC,画出图形写出点N的坐标为 ;
BC,画出图形写出点N的坐标为 ;
(3)连接AE、EF得△AEF.请按步骤完成作图,并写出△AEF的面积为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com