
【题目】如图,已知梯形ABCD中,AD∥BC,AC、BD相交于点O,AB⊥AC,AD=CD,AB=3,BC=5.求:
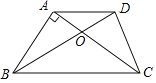
(1)tan∠ACD的值;
(2)梯形ABCD的面积.
【答案】(1)![]() ;(2)9
;(2)9
【解析】
(1)作DE∥AB交BC于E,交AC于M,证出DE⊥AC,由等腰三角形的性质得出AM=CM,证明四边形ABCD是平行四边形,得出DE=AB=3,在Rt△ABC中,由勾股定理求出AC=4,得出AM=CM=2,由平行线分线段成比例可得出DM与EM,即可求出答案
(2)梯形ABCD的面积=△ABC的面积+△ACD的面积,即可求出答案
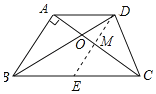
(1)作DE∥AB交BC于E,交AC于M,如图所示:
∵AB⊥AC,DE∥AB,
∴DE⊥AC,
∵AD=CD,
∴AM=CM,
∵AD∥BC,DE∥AB,
∴四边形ABED是平行四边形,
∴DE=AB=3,
在Rt△ABC中, ![]() ,
,
∴AM=CM=2,
∵AD∥BC,
∴DM:EM=AM:CM=1:1,
∴![]() ,
,
∴ ;
;
(2)梯形ABCD的面积=△ABC的面积+△ACD的面积![]() .
.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
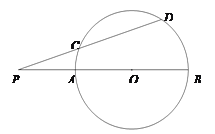
【题目】已知P是![]() 的直径BA延长线上的一个动点,∠P的另一边交
的直径BA延长线上的一个动点,∠P的另一边交![]() 于点C、D,两点位于AB的上方,
于点C、D,两点位于AB的上方,![]() =6,OP=m,
=6,OP=m,![]() ,如图所示.另一个半径为6的
,如图所示.另一个半径为6的![]() 经过点C、D,圆心距
经过点C、D,圆心距![]() .
.
(1)当m=6时,求线段CD的长;
(2)设圆心O1在直线![]() 上方,试用n的代数式表示m;
上方,试用n的代数式表示m;
(3)△POO1在点P的运动过程中,是否能成为以OO1为腰的等腰三角形,如果能,试求出此时n的值;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
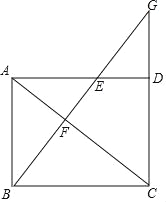
【题目】已知:如图,在平行四边形ABCD中,AC为对角线,E是边AD上一点,BE⊥AC交AC于点F,BE、CD的延长线交于点G,且∠ABE=∠CAD.
(1)求证:四边形ABCD是矩形;
(2)如果AE=EG,求证:AC2=BCBG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的边AB是⊙O的直径,点C在⊙O上,已知AC=6cm,BC=8cm,点P、Q分别在边AB、BC上,且点P不与点A、B重合,BQ=kAP(k>0),联接PC、PQ.
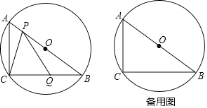
(1)求⊙O的半径长;
(2)当k=2时,设AP=x,△CPQ的面积为y,求y关于x的函数关系式,并写出定义域;
(3)如果△CPQ与△ABC相似,且∠ACB=∠CPQ,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:以O为圆心的扇形AOB中,∠AOB=90°,点C为![]() 上一动点,射线AC交射线OB于点D,过点D作OD的垂线交射线OC于点E,联结AE.
上一动点,射线AC交射线OB于点D,过点D作OD的垂线交射线OC于点E,联结AE.

(1)如图1,当四边形AODE为矩形时,求∠ADO的度数;
(2)当扇形的半径长为5,且AC=6时,求线段DE的长;
(3)联结BC,试问:在点C运动的过程中,∠BCD的大小是否确定?若是,请求出它的度数;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
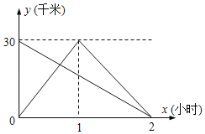
【题目】在一条笔直的公路上有AB两地,小明骑自行车从A地去B地,小刚骑电动车从B地去A地然后立即原路返回到B地,如图是两人离B地的距离y(千米)和行驶时间x(小时)之间的函数图象.请根据图象回答下列问题:
(1)AB两地的距离是_____,小明行驶的速度是_____.
(2)若两人间的距离不超过3千米时,能够用无线对讲机保持联系,那么小刚从A地原路返回到B地途中,两人能够用无线对讲机保持联系的x的取值范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△BEC均为等腰直角三角形,且∠ACB=∠BEC=90°,AC=4![]() ,点P为线段BE延长线上一点,连接CP以CP为直角边向下作等腰直角△CPD,线段BE与CD相交于点F.
,点P为线段BE延长线上一点,连接CP以CP为直角边向下作等腰直角△CPD,线段BE与CD相交于点F.

(1)求证:![]() ;
;
(2)连接BD,请你判断AC与BD有什么位置关系?并说明理由;
(3)若PE=1,求△PBD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,
,![]() ,在
,在![]() 的延长线上任取一点
的延长线上任取一点![]() ,过点
,过点![]() 作
作![]() 的平行线交
的平行线交![]() 的延长线于点
的延长线于点![]() .
.
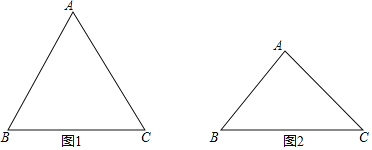
(1)当![]() 时,如图1,依题意补全图形,直接写出
时,如图1,依题意补全图形,直接写出![]() ,
,![]() ,
,![]() 的数量关系;
的数量关系;
(2)当![]() 时,如图2,判断
时,如图2,判断![]() ,
,![]() ,
,![]() 之间的数量关系,并加以证明;
之间的数量关系,并加以证明;
(3)当![]() 时(
时(![]() ),请写出
),请写出![]() ,
,![]() ,
,![]() 之间的数量关系并写出解题思路.
之间的数量关系并写出解题思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+(a+2)x+2(a≠0),与x轴交于点A(4,0),与y轴交于点B,在x轴上有一动点P(m,0)(0<m<4),过点P作x轴的垂线交直线AB于点N,交抛物线于点M.
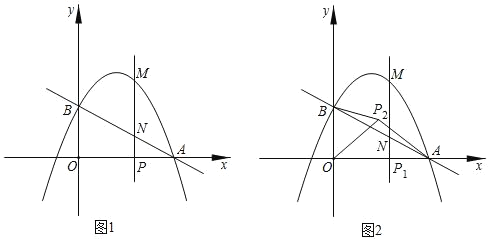
(1)求抛物线的解析式;
(2)若PN:PM=1:4,求m的值;
(3)如图2,在(2)的条件下,设动点P对应的位置是P1,将线段OP1绕点O逆时针旋转得到OP2,旋转角为α(0°<α<90°),连接AP2、BP2,求AP2+![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com