
【题目】已知:以O为圆心的扇形AOB中,∠AOB=90°,点C为![]() 上一动点,射线AC交射线OB于点D,过点D作OD的垂线交射线OC于点E,联结AE.
上一动点,射线AC交射线OB于点D,过点D作OD的垂线交射线OC于点E,联结AE.

(1)如图1,当四边形AODE为矩形时,求∠ADO的度数;
(2)当扇形的半径长为5,且AC=6时,求线段DE的长;
(3)联结BC,试问:在点C运动的过程中,∠BCD的大小是否确定?若是,请求出它的度数;若不是,请说明理由.
【答案】(1) 30°;(2) ![]() ;(3)能,45o,理由见解析
;(3)能,45o,理由见解析
【解析】
(1)利用矩形的性质,证明△OAC是等边三角形即可得出答案
(2)作OH⊥AD于H,由△AOH∽△ADO,可求AD的值,从而可以求出CD的值,再由DE∥OA,即可求出DE
(3)连接AB、BC,即可求出答案
(1)如图1中,

∵四边形ABCD是矩形,
∴AD=EC,AC=CD,OC=CE,∠AOD=90°
∴AC=OC=OA,
∴△AOC是等边三角形,
∴∠OAD=60°,
∴∠ADO=90°﹣∠OAD=30°.
(2)如图2中,作OH⊥AD于H.

∵OA=OC,OH⊥AC,
∴AH=HC=3,
∵∠OAH=∠OAD,∠AHO=∠AOD,
∴△AOH∽△ADO,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵DE⊥OD,
∴∠EDO=90°,
∴∠AOD+∠EDO=180°,
∴DE∥OA,
∴![]() ,
,
∴ ,
,
∴![]() .
.
(3)如图3中,结论:∠BCD的值是确定的.∠BCD=45°.
理由:连接AB、BC.

∵∠BCD=∠BAC+∠ABC,
又∵![]() ,
,
∴![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】自1993年起,联合国将每年的3月22日定为“世界水日”,宗旨是唤起公众的节水意识,加强水资源保护.某校在开展“节约每一滴水”的活动中,从初三年级随机选出20名学生统计出各自家庭一个月的节约用水量,有关数据整理如下表.
节约用水量(单位:吨) | 1 | 1.2 | 1.4 | 2 | 2.5 |
家庭数 | 4 | 6 | 5 | 3 | 2 |
这组数据的中位数和众数分别是( )
A. 1.2,1.2; B. 1.4,1.2; C. 1.3,1.4; D. 1.3,1.2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在半径为2的扇形![]() 中,
中,![]() °,点C在半径OB上,AC的垂直平分线交OA于点D,交弧AB于点E,联结
°,点C在半径OB上,AC的垂直平分线交OA于点D,交弧AB于点E,联结![]() .
.
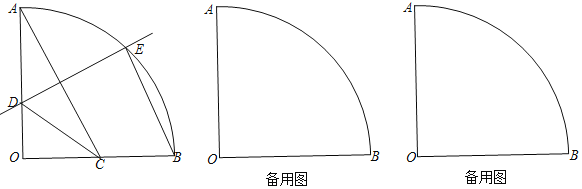
(1)若C是半径OB中点,求![]() 的正弦值;
的正弦值;
(2)若E是弧AB的中点,求证:![]() ;
;
(3)联结CE,当△DCE是以CD为腰的等腰三角形时,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A.一组数据﹣2,﹣1,0,1,1,2的中位数是0
B.质检部门要了解一批灯泡的使用寿命,应当采用普查的调查方式
C.购买一张福利彩票中奖是一个确定事件
D.分别写有三个数字﹣1,﹣2,4的三张卡片(卡片的大小形状都相同),从中任意抽取两张,则卡片上的两数之积为正数的概率为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果市场的甲、乙两家商店中都有批发某种水果,批发该种水果x千克时,在甲、乙两家商店所花的钱分别为y1元和y2元,已知y1、y2关于x的函数图象分别为如图所示的折线OAB和射线OC.

(1)当x的取值为 时,在甲乙两家店所花钱一样多?
(2)当x的取值为 时,在乙店批发比较便宜?
(3)如果批发30千克该水果时,在甲店批发比在乙店批发便宜50元,求射线AB的表达式,并写出定义域.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知梯形ABCD中,AD∥BC,AC、BD相交于点O,AB⊥AC,AD=CD,AB=3,BC=5.求:
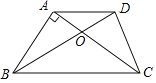
(1)tan∠ACD的值;
(2)梯形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
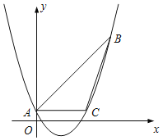
【题目】如图,已知抛物线y=ax2﹣2x+c经过△ABC的三个顶点,其中点A(0,1),点B(9,10),AC∥x轴.
(1)求这条抛物线的解析式.
(2)求tan∠ABC的值.
(3)若点D为抛物线的顶点,点E是直线AC上一点,当△CDE与△ABC相似时,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
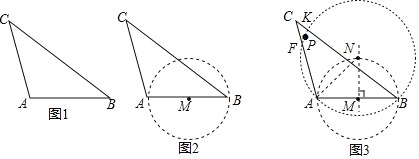
【题目】在数学课上,老师布置了一项作图任务,如下:
已知:如图1,在![]() 中,
中,![]() ,请在图中的
,请在图中的![]() 内(含边),画出使
内(含边),画出使![]() 的一个点
的一个点![]() (保留作图痕迹),小红经过思考后,利用如下的步骤找到了点
(保留作图痕迹),小红经过思考后,利用如下的步骤找到了点![]() :
:
(1)以![]() 为直径,作
为直径,作![]() ,如图2;
,如图2;
(2)过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 于点
于点![]() ;
;
(3)以点![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() ,分别交
,分别交![]() 、
、![]() 边于
边于![]() 、
、![]() ,在劣弧
,在劣弧![]() 上任取一点
上任取一点![]() 即为所求点,如图3,说出此种作法的依据 _______________.
即为所求点,如图3,说出此种作法的依据 _______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=BC,以AB为直径的⊙O与AC相交于点D,过点D作DE⊥BC交AB延长线于点E,垂足为点F.
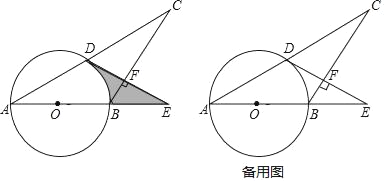
(1)证明:DE是⊙O的切线;
(2)若BE=4,∠E=30°,求由![]() 、线段BE和线段DE所围成图形(阴影部分)的面积,
、线段BE和线段DE所围成图形(阴影部分)的面积,
(3)若⊙O的半径r=5,sinA=![]() ,求线段EF的长.
,求线段EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com