
����Ŀ����ͼ����ABC�ı�AB�ǡ�O��ֱ������C�ڡ�O�ϣ���֪AC��6cm��BC��8cm����P��Q�ֱ��ڱ�AB��BC�ϣ��ҵ�P�����A��B�غϣ�BQ��kAP��k��0��������PC��PQ��
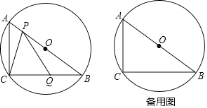
��1�����O�İ뾶����
��2����k��2ʱ����AP��x����CPQ�����Ϊy����y����x�ĺ�����ϵʽ����д��������
��3�������CPQ����ABC���ƣ��ҡ�ACB����CPQ����k��ֵ��
���𰸡���1��5����2��y=![]() ;��3��
;��3��![]()
��������
��1������֤����ACB��90����Ȼ�����ù��ɶ������ɽ�����⣻
��2����ͼ2�У���PH��BC��H����PH��AC�����Ƴ�![]() ���Ƴ�
���Ƴ�![]() ���ó�
���ó�![]() ������
������![]() ���㼴�ɣ�
���㼴�ɣ�
��3����Ϊ��CPQ����ABC���ƣ���CPQ����ACB��90��������Ϊ��CQP����B��
����ֻ�С�PCB����B���Ƴ�PC��PB���ɡ�B+��A��90������ACP+��PCB��90����
�Ƴ���A����ACP���ó�PA��PC��PB��5���ɡ�COQ�ס�BCA���Ƴ�![]() ��
��
�Ƴ�![]() �����ɽ������.
�����ɽ������.
��1����AB��ֱ����
���ACB��90������AC��6��BC��8��
��![]() ��
��
���O�İ뾶Ϊ5��
��2����ͼ2�У���PH��BC��H��

��PH��AC��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��3����ͼ2�У�

�ߡ�CPQ����ABC���ƣ���CPQ����ACB��90����
�֡ߡ�CQP����B��
��ֻ�С�PCB����B��
��PC��PB��
�ߡ�B+��A��90������ACP+��PCB��90����
���A����ACP��
��PA��PC��PB��5��
���COQ�ס�BCA��
��![]() ��
��
��![]() ��
��
��![]() ��
��


 ͨ��ѧ��Ĭд����ϵ�д�
ͨ��ѧ��Ĭд����ϵ�д� ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
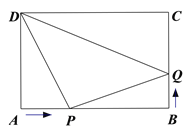
����Ŀ����ͼ���ھ���ABCD�У�AB=10cm,AD=8cm,��P�ӵ�A������AB��2cm/s���ٶ�����յ�B�˶���ͬʱ��Q�ӵ�B������BC��1cm/s���ٶ�����յ�C�˶������ǵ����յ��ֹͣ�˶�.
(1)�����P��D�ľ����ǵ�P��Q�ľ����2����
(2)�����DPQ�������24cm2.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���![]() ��ͼ����
��ͼ����![]() �ύ��
�ύ��![]() ��
��![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��![]() �������Ϊ
�������Ϊ![]() ��
��
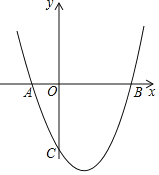
��1������κ����Ľ���ʽ��
��2������![]() ���������ڵ��������ϵ�һ�����㣬���ı���
���������ڵ��������ϵ�һ�����㣬���ı���![]() ��������ʱ�����
��������ʱ�����![]() �����꣬������ı���
�����꣬������ı���![]() ����������
����������
��3����![]() Ϊ�����߶Գ�����һ���㣬ֱ��д��ʹ
Ϊ�����߶Գ�����һ���㣬ֱ��д��ʹ![]() Ϊֱ�������εĵ�
Ϊֱ�������εĵ�![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ԲO��ֱ��AB��10����һ������Ϊ6�Ķ���CD�ڻ�AB�ϻ�������C����D�ֱ����A����B�غϣ�����E��F��AB�ϣ�EC��CD��FD��CD��
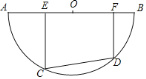
��1����֤��EO��OF��
��2������OC�������ECO����һ���ڽǵ���45�㣬���߶�EF�ij���
��3��������CD�ڻ�AB�ϻ���ʱ�������CE��x���ı���CDFE���ΪS���ܳ�Ϊl���ʣ�S��l�Ƿ�ֱ�����x�ı仯���仯��������ѧ�ĺ���֪ʶֱ��д�����ǵĺ�������ʽ��������������˵����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���У���ȷ���ǣ�������
A.һ�����ݩ�2����1��0��1��1��2����λ����0
B.�ʼ첿��Ҫ�˽�һ�����ݵ�ʹ��������Ӧ�������ղ�ĵ��鷽ʽ
C.����һ�Ÿ�����Ʊ�н���һ��ȷ���¼�
D.�ֱ�д���������֩�1����2��4�����ſ�Ƭ����Ƭ�Ĵ�С��״����ͬ�������������ȡ���ţ���Ƭ�ϵ�����֮��Ϊ�����ĸ���Ϊ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ı���ABCD�У�DB��BC��DBƽ�֡�ADC����EΪ��CD���е㣬AB��BE��
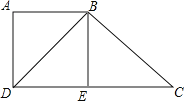
��1����֤��BD2��ADDC��
��2������AE����BD��BCʱ����֤��ABCEΪƽ���ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����ABCD�У�AD��BC��AC��BD�ཻ�ڵ�O��AB��AC��AD��CD��AB��3��BC��5����
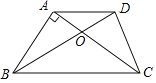
��1��tan��ACD��ֵ��
��2������ABCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
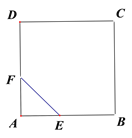
����Ŀ����ͼ��E��F�ֱ�Ϊ������ABCD�ı�AB��AD�ϵĵ㣬��AE=AF������EF������AEF�Ƶ�A��ʱ����ת45�㣬ʹE����E![]() ��F����F
��F����F![]() ������BE
������BE![]() ���ӳ���DF
���ӳ���DF![]() �ڵ�G�����AB=
�ڵ�G�����AB=![]() ��AE=1����DG=______.
��AE=1����DG=______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
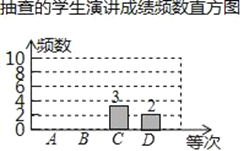
����Ŀ��ijУΪ��ף�����������������2018��4�µ���֯��Уѧ���ٰ������������ľ�����г�����������ݽ�������Ϊ�˽�ѧ�����ݽ������еijɼ������ѧУ�����ȡ�˲���ѧ�����ݽ������ɼ�����ͳ��(���֣�100�֣��ȴΣ�A�����㣺90��100�֣�B�����ã�80��89�֣�C��һ�㣺60��79�֣�D���ϲ60�����£�����60��)�õ����²�������ͼ����
�ȴ� | Ƶ�� | Ƶ�� |
A | a | 0.25 |
B | b | 0.5 |
C | 3 | m |
D | 2 | 0.1 |
����������Ϣ�����������
(1)����a��_____��b��_____��m��_______������ȫƵ���ֲ�ֱ��ͼ��
(2)���ݳ��ѧ���ݽ��ɼ�Ƶ��ͳ�Ʊ�����������ͳ��ͼ�У���ʾC�ȴβ��ֵ��������ĽǵĶ�����_______��
(3)��A�ȴ�����2��Ů��������Ϊ������ѧУ����A�ȴ�ѧ���г�ȡ2��ѧ������ݽ���ϲμ�ȫ�����������걭���ݽ���������ǡ�ó�ȡ1��������1��Ů���ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com