
【题目】如图,△ABC和△BEC均为等腰直角三角形,且∠ACB=∠BEC=90°,AC=4![]() ,点P为线段BE延长线上一点,连接CP以CP为直角边向下作等腰直角△CPD,线段BE与CD相交于点F.
,点P为线段BE延长线上一点,连接CP以CP为直角边向下作等腰直角△CPD,线段BE与CD相交于点F.

(1)求证:![]() ;
;
(2)连接BD,请你判断AC与BD有什么位置关系?并说明理由;
(3)若PE=1,求△PBD的面积.
【答案】(1)见解析;(2) AC∥BD,理由见解析;(3)![]()
【解析】
(1)直接利用相似三角形的判定方法得出△BCE∽△DCP,进而得出答案;
(2)首先得出△PCE∽△DCB,进而求出∠ACB=∠CBD,即可得出AC与BD的位置关系;
(3)首先利用相似三角形的性质表示出BD,PM的长,进而根据三角形的面积公式得到△PBD的面积.
(1)证明:∵△BCE和△CDP均为等腰直角三角形,
∴∠ECB=∠PCD=45°,∠CEB=∠CPD=90°,
∴△BCE∽△DCP,
∴![]() ;
;
(2)解:结论:AC∥BD,
理由:∵∠PCE+∠ECD=∠BCD+∠ECD=45°,
∴∠PCE=∠BCD,
又∵![]() ,
,
∴△PCE∽△DCB,
∴∠CBD=∠CEP=90°,
∵∠ACB=90°,
∴∠ACB=∠CBD,
∴AC∥BD;
(3)解:如图所示:作PM⊥BD于M,
∵AC=4![]() ,△ABC和△BEC均为等腰直角三角形,
,△ABC和△BEC均为等腰直角三角形,
∴BE=CE=4,
∵△PCE∽△DCB,
∴![]() ,即
,即![]() ,
,
∴BD=![]() ,
,
∵∠PBM=∠CBD﹣∠CBP=45°,BP=BE+PE=4+1=5,
∴PM=5sin45°=![]()
∴△PBD的面积S=![]() BDPM=
BDPM=![]() ×
×![]() ×
×![]() =
=![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,![]() 是直角三角形,
是直角三角形,![]() .
.
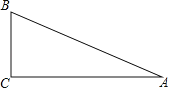
(1)动手操作:利用尺规作![]() 的平分线,交
的平分线,交![]() 于点
于点![]() ,再以
,再以![]() 为圆心,
为圆心,![]() 的长为半径作
的长为半径作![]() (保留作图痕迹,不写作法);
(保留作图痕迹,不写作法);
(2)综合运用:请根据所作的图,
①判断![]() 与
与![]() 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
②若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A.一组数据﹣2,﹣1,0,1,1,2的中位数是0
B.质检部门要了解一批灯泡的使用寿命,应当采用普查的调查方式
C.购买一张福利彩票中奖是一个确定事件
D.分别写有三个数字﹣1,﹣2,4的三张卡片(卡片的大小形状都相同),从中任意抽取两张,则卡片上的两数之积为正数的概率为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知梯形ABCD中,AD∥BC,AC、BD相交于点O,AB⊥AC,AD=CD,AB=3,BC=5.求:
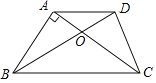
(1)tan∠ACD的值;
(2)梯形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
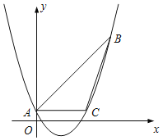
【题目】如图,已知抛物线y=ax2﹣2x+c经过△ABC的三个顶点,其中点A(0,1),点B(9,10),AC∥x轴.
(1)求这条抛物线的解析式.
(2)求tan∠ABC的值.
(3)若点D为抛物线的顶点,点E是直线AC上一点,当△CDE与△ABC相似时,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
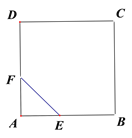
【题目】如图,E、F分别为正方形ABCD的边AB、AD上的点,且AE=AF,联接EF,将△AEF绕点A逆时针旋转45°,使E落在E![]() ,F落在F
,F落在F![]() ,联接BE
,联接BE![]() 并延长交DF
并延长交DF![]() 于点G,如果AB=
于点G,如果AB=![]() ,AE=1,则DG=______.
,AE=1,则DG=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
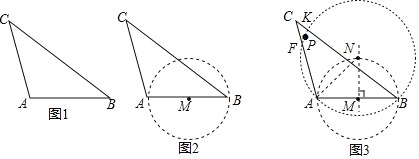
【题目】在数学课上,老师布置了一项作图任务,如下:
已知:如图1,在![]() 中,
中,![]() ,请在图中的
,请在图中的![]() 内(含边),画出使
内(含边),画出使![]() 的一个点
的一个点![]() (保留作图痕迹),小红经过思考后,利用如下的步骤找到了点
(保留作图痕迹),小红经过思考后,利用如下的步骤找到了点![]() :
:
(1)以![]() 为直径,作
为直径,作![]() ,如图2;
,如图2;
(2)过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 于点
于点![]() ;
;
(3)以点![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() ,分别交
,分别交![]() 、
、![]() 边于
边于![]() 、
、![]() ,在劣弧
,在劣弧![]() 上任取一点
上任取一点![]() 即为所求点,如图3,说出此种作法的依据 _______________.
即为所求点,如图3,说出此种作法的依据 _______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,若点P和点![]() 关于y轴对称,点
关于y轴对称,点![]() 和点
和点![]() 关于直线l对称,则称点
关于直线l对称,则称点![]() 是点P关于y轴,直线l的二次对称点.
是点P关于y轴,直线l的二次对称点.
![]() 如图1,点
如图1,点![]() .
.
![]() 若点B是点A关于y轴,直线
若点B是点A关于y轴,直线![]() :
:![]() 的二次对称点,则点B的坐标为______;
的二次对称点,则点B的坐标为______;
![]() 若点
若点![]() 是点A关于y轴,直线
是点A关于y轴,直线![]() :
:![]() 的二次对称点,则a的值为______;
的二次对称点,则a的值为______;
![]() 若点
若点![]() 是点A关于y轴,直线
是点A关于y轴,直线![]() 的二次对称点,则直线
的二次对称点,则直线![]() 的表达式为______;
的表达式为______;
![]() 如图2,
如图2,![]() 的半径为
的半径为![]() 若
若![]() 上存在点M,使得点
上存在点M,使得点![]() 是点M关于y轴,直线
是点M关于y轴,直线![]() :
:![]() 的二次对称点,且点
的二次对称点,且点![]() 在射线
在射线![]() 上,b的取值范围是______;
上,b的取值范围是______;
![]() 是x轴上的动点,
是x轴上的动点,![]() 的半径为2,若
的半径为2,若![]() 上存在点N,使得点
上存在点N,使得点![]() 是点N关于y轴,直线
是点N关于y轴,直线![]() :
:![]() 的二次对称点,且点
的二次对称点,且点![]() 在y轴上,求t的取值范围.
在y轴上,求t的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com