
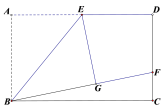
【题目】如图,矩形ABCD中,E是AD的中点,将![]() 沿直线BE折叠后得到
沿直线BE折叠后得到![]() ,延长BG交CD于点F,若
,延长BG交CD于点F,若![]() 则FD的长为( )
则FD的长为( )
A. 1B. 2C. ![]() D.
D. ![]()
【答案】B
【解析】
根据点E是AD的中点以及翻折的性质可以求出AE=DE=EG,然后利用“HL”证明△EDF和△EGF全等,根据全等三角形对应边相等可证得DF=GF;设FD=x,表示出FC、BF,然后在Rt△BCF中,利用勾股定理列式进行计算即可得解.
解:∵E是AD的中点,
∴AE=DE,
∵△ABE沿BE折叠后得到△GBE,
∴AE=EG,AB=BG,
∴ED=EG,
∵在矩形ABCD中,
∴∠A=∠D=90°,
∴∠EGF=90°,
连接EF,
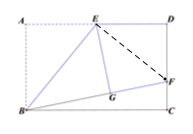
∵在Rt△EDF和Rt△EGF中,
![]() ,
,
∴Rt△EDF≌Rt△EGF(HL),
∴DF=FG,
设DF=x,则BF=3+x,CF=3-x,
在Rt△BCF中,BC2+CF2=BF2,即(2![]() )2+(3-x)2=(3+x)2,
)2+(3-x)2=(3+x)2,
解得:x=2,
即DF=2;
故选:B.


科目:初中数学 来源: 题型:
【题目】小明和小亮玩一个游戏:三张大小、质地都相同的卡片上分别标有数字2,3,4(背面完全相同),现将标有数字的一面朝下.小明从中任意抽取一张,记下数字后放回洗匀,然后小亮从中任意抽取一张,计算小明和小亮抽得的两个数字之和.若和为奇数,则小明胜;若和为偶数,则小亮胜.
(1)请你用画树状图或列表的方法,求出这两数和为6的概率.
(2)你认为这个游戏规则对双方公平吗?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极绘就我市“一福地、四名城”建设的宏伟蓝图,某镇大力发展旅游业,一店铺专门售卖地方特产“曲山老鹅”,以往销售数据表明,该“曲山老鹅”每天销售数量y(只)与销售单价x(元)满足一次函数y=-![]() x+110,每只“曲山老鹅”各项成本合计为20元/只.
x+110,每只“曲山老鹅”各项成本合计为20元/只.
(1)该店铺“曲山老鹅”销售单价x定为多少时,每天获利最大?最大利润是多少?
(2)该店店主关心教育,决定今后的一段时间从每天的销售利润中捐出200元给当地学校作为本学期优秀学生的奖励资金,为了保证该店捐款后每天剩余利润不低于4000元,试确定该“曲山老鹅”销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
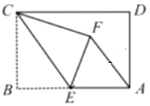
【题目】矩形ABCD中,AB=4,BC=3,点E为AB的中点,将矩形ABCD沿CE折叠,使得点B落到点F的位置.
(1)求证:AF∥CE.
(2)求AF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝即将到来的“三月三”壮族传统节日,某校举行了书法比赛,赛后随机抽查部分参赛同学的成绩,并制作成如下图表:
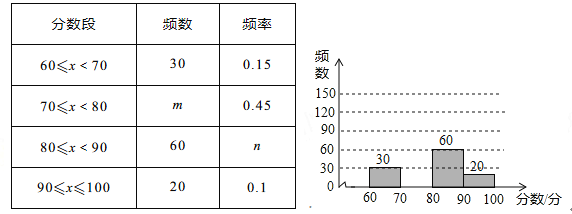
请根据如上图表提供的信息,解答下列问题:
(1)这次随机抽查了 名学生,表中的数![]() .
.![]() .
.
(2)请在图中补全频数分布直方图;
(3)若绘制扇形统计图,分数段![]() 所对应扇形的圆心角为 度;
所对应扇形的圆心角为 度;
(4)全校共有![]() 名学生参加比赛,估计该校成绩
名学生参加比赛,估计该校成绩![]() 范围内的学生有多少人?
范围内的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ΔABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC.
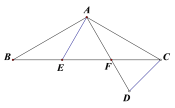
(1)求证:ΔABE≌ΔACF;
(2)若∠BAE=30°,则∠ADC= (直接写答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程1﹣(x﹣a)(x﹣b)=0的两根,且a<b,则a、b、m、n的大小关系是( ).
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以OA1对角线为边作正方形OA1A2B1,再以正方形的对角线OA2作正方形OA1A2B1,…,依次规律,则点A8的坐标是_____.
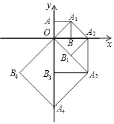
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com