
【题目】为庆祝即将到来的“三月三”壮族传统节日,某校举行了书法比赛,赛后随机抽查部分参赛同学的成绩,并制作成如下图表:
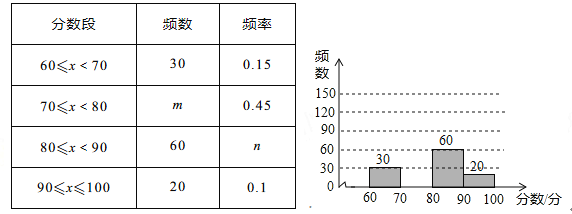
请根据如上图表提供的信息,解答下列问题:
(1)这次随机抽查了 名学生,表中的数![]() .
.![]() .
.
(2)请在图中补全频数分布直方图;
(3)若绘制扇形统计图,分数段![]() 所对应扇形的圆心角为 度;
所对应扇形的圆心角为 度;
(4)全校共有![]() 名学生参加比赛,估计该校成绩
名学生参加比赛,估计该校成绩![]() 范围内的学生有多少人?
范围内的学生有多少人?
 能力评价系列答案
能力评价系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC=4,P是△ABC的高CD上一个动点,以B点为旋转中心把线段BP逆时针旋转45°得到BP′,连接DP′,则DP′的最小值是( )
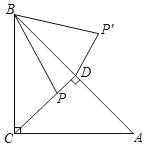
A.2![]() -2B.4﹣2
-2B.4﹣2![]() C.2﹣
C.2﹣![]() D.
D.![]() -1
-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于二次函数y=-x2-2x+3说法正确的是( )
A. 当![]() 时,函数最大值4
时,函数最大值4
B. 当![]() 时,函数最大值2
时,函数最大值2
C. 将其图象向上平移3个单位后,图象经过原点
D. 将其图象向左平移3个单位后,图象经过原点
查看答案和解析>>
科目:初中数学 来源: 题型:
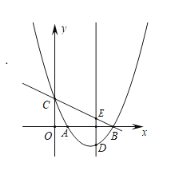
【题目】在平面直角坐标系中,已知抛物线y=ax2+bx+c(a≠0)经过点A(1,0).B(4,0),C(0,2)三点,直线y=kx+t经过B.C两点,点D是抛物线上一个动点,过点D作y轴的平行线,与直线BC相交于点E.
(1)求直线和抛物线的解析式;
(2)当点D在直线BC下方的抛物线上运动,使线段DE的长度最大时,求点D的坐标;
(3)点D在运动过程中,若使O.C.D.E为顶点的四边形为平行四边形时,请直接写出满足条件的所有点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
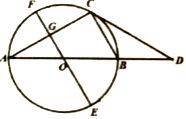
【题目】如图,⊙O是△ABC的外接圆,AB为⊙O的直径,过点C作∠BCD=∠CAB交AB的延长线于点D,过点O作直径EF∥BC,交AC于点G.
(1)求证:CD是⊙O的切线.
(2)若⊙O的半径为2,∠BCD=30°.
①连接AE、DE,求证:四边形ACDE是菱形.
②当点P是线段AD上的一动点时,求PF+PG的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
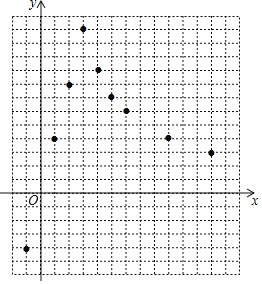
【题目】初三某班同学小戴想根据学习函数的经验,通过研究一个未学过的函数的图象,从而探究其各方面性质.
下表是函数y与自变量x的几组对应值:
x | … | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 9 | 12 | … |
y | … | -4 | 0 | 4 | 8 | 12 | 9 | 7.2 | 6 | 4 | 3 | … |
(1)在平面直角坐标系xOy中,每个小正方形的边长为一个单位长度,描出了以上表中各对对应值为坐标的点,请根据描出的点,画出该函数的图象.
(2)请根据画出的函数图象,直接写出该函数的关系式y=______(请写出自变量的取值范围),并写出该函数的一条性质:______.
(3)当直线y=-![]() x+b与该函数图象有3个交点时,求b的取值范围.
x+b与该函数图象有3个交点时,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
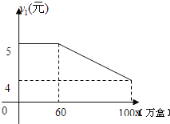
【题目】有一个茶叶厂,该厂的茶叶主要有两种销售方式,一种方式是卖给茶叶经销商,另一种方式是在各超市的柜台进行销售,每年该厂生产的茶叶都可以全部销售,该茶叶厂每年可以生产茶叶100万盒,其中,卖给茶叶经销商每盒茶叶的利润y1(元)与销售量x(万盒)之间的函数关系如图15所示;在各超市柜台销售的每盒利润y2(元)与销售量x(万盒)之间的函数关系为:当0≤x<40时, y2=—0.75x+80,
当40≤x≤100时 y2=40.
(1)写出该茶叶厂卖给茶叶经销商的销售总利润z1(万元)与其销售量x(万盒)之间的函数关系式,并指出x的取值范围;
(2)写出该茶叶厂在各超市柜台销售的总利润z2(万元)与卖给茶叶经销商的销售量x(万盒)之间的函数关系式及x取值范围;
(3)求该茶叶厂每年的总利润w(万元)与卖给茶叶经销商的销售量x(万盒)之间的函数关系式,并帮助该茶叶厂确定卖给茶叶经销商和在各超市柜台的销量各为多少万盒时,该公司的年利润最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com