
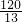 cm
cm ×底×高,可求得S△ABD、S△ACD、S△ABC;又由图易知,S△ABC=S△ABD+S△ACD,则DE+DF=CG,然后根据勾股定理得CG2=AC2-AG2=BC2-BG2,设AG=xcm,则列出关于x的方程132-x2=102-(13-x)2,解方程求出x的值,进而可求出结果.
×底×高,可求得S△ABD、S△ACD、S△ABC;又由图易知,S△ABC=S△ABD+S△ACD,则DE+DF=CG,然后根据勾股定理得CG2=AC2-AG2=BC2-BG2,设AG=xcm,则列出关于x的方程132-x2=102-(13-x)2,解方程求出x的值,进而可求出结果.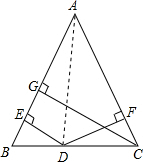 ,在△ABC中,AB=AC=13cm,BC=10cm,D为BC上任意一点,DE⊥AB,DF⊥AC,垂足为E、F.
,在△ABC中,AB=AC=13cm,BC=10cm,D为BC上任意一点,DE⊥AB,DF⊥AC,垂足为E、F. AB•ED;
AB•ED; AC•DF;
AC•DF; AB•CG;
AB•CG; AB•CG=
AB•CG= AB•ED+
AB•ED+ AC•DF,
AC•DF,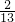 .
.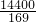 ,
,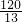 .
.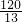 .
.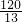 cm.
cm.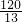 cm.
cm.

 通城学典默写能手系列答案
通城学典默写能手系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com