
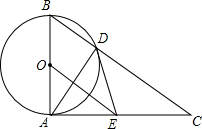
 如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.
如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.分析 (1)如图,连接OD.通过证明△AOE≌△DOE得到∠OAE=∠ODE=90°,易证得结论;
(2)在Rt△OAE中,由OA=3,OE=6,得出cos∠AOE=$\frac{1}{2}$,得出∠AOE=60°,进而求得AE的长和∠AOD=120°,然后根据S四边形OAED-S扇形OAD即可求得线段AE、线段DE和弧AD围成的图形的面积.
解答 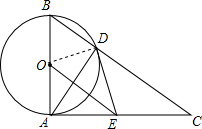 (1)证明:如图,连接OD.
(1)证明:如图,连接OD.
∵AC⊥AB,
∴∠BAC=90°,即∠OAE=90°.
在△AOE与△DOE中,
$\left\{\begin{array}{l}{OA=OD}\\{OE=OE}\\{AE=DE}\end{array}\right.$,
∴△AOE≌△DOE(SSS),
∴∠OAE=∠ODE=90°,即OD⊥ED.
又∵OD是⊙O的半径,
∴ED是⊙O的切线;
(2)解:如图,在Rt△OAE中,OA=3,OE=6,
∴$cos∠AOE=\frac{3}{6}=\frac{1}{2}$,
∴∠AOE=60°,
∴∠AOD=120°,AE=OE•sin∠AOE=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
∴S△AOE=$\frac{1}{2}$AE•OA=$\frac{1}{2}$×3$\sqrt{3}$×3=$\frac{9\sqrt{3}}{2}$,
∴S四边形OAED=2S△AOE=9$\sqrt{3}$,
∴线段AE、线段DE和弧AD围成的图形的面积=S四边形OAED-S扇形OAD
=9$\sqrt{3}$-$\frac{120π×{3}^{2}}{360}$
=9$\sqrt{3}$-3π.
点评 本题考查了切线的判定以及扇形的面积,求得△AOE≌△DOE和∠AOE=60°是解题的关键.


科目:初中数学 来源:2016-2017学年江苏省句容市华阳片八年级下学期第一次月考数学试卷(解析版) 题型:解答题
某学校开展课外球类特色的体育活动,决定开设A:羽毛球、B:篮球、C:乒乓球、 D:足球四种球类项目.为了解学生最喜欢哪一种活动项目(每人只选取一种),随机抽取了部分学生进行调查,并将调查结果绘成如甲、乙所示的统计图,请你结合图中信息解答下列问题.
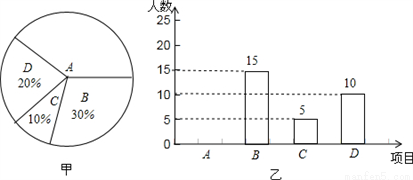
(1)样本中最喜欢A项目的人数所占的百分比为 ,其所在扇形统计图中对应的圆心角度数是 度;
(2)请把条形统计图补充完整;
(3)若该校有学生3000人,请根据样本估计全校最喜欢足球的学生人数约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
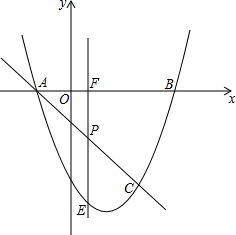 如图所示,抛物线y=x2-3x-4与x轴交于A,B两点(A点在B点左侧),直线y=kx-1与抛物线y=x2-3x-4交于A,C两点.求A,B,C三点的坐标.
如图所示,抛物线y=x2-3x-4与x轴交于A,B两点(A点在B点左侧),直线y=kx-1与抛物线y=x2-3x-4交于A,C两点.求A,B,C三点的坐标.查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省句容市华阳片八年级下学期第一次月考数学试卷(解析版) 题型:单选题
如图,由两个长为9,宽为3的全等矩形叠合而得到四边形ABCD,则四边形ABCD面积的最大值是( ).
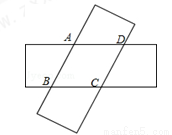
A. 15 B. 16 C. 19 D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
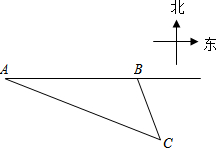 如图,我渔政船在东海海面上自西向东匀速巡航,在A地观测到某海岛C在东偏南21.3°方向上.若渔政船继续向东航行60海里到达B处,此时观测到海岛C在东偏南63.5°方向上.之后,渔政船再向东航多少海里,离海岛C的距离最近?
如图,我渔政船在东海海面上自西向东匀速巡航,在A地观测到某海岛C在东偏南21.3°方向上.若渔政船继续向东航行60海里到达B处,此时观测到海岛C在东偏南63.5°方向上.之后,渔政船再向东航多少海里,离海岛C的距离最近?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=8.3}\\{y=1.2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=10.3}\\{y=1.2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=6.3}\\{y=2.2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=10.3}\\{y=0.2}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com