
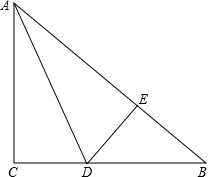
 如图所示,已知在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB于点E,△DEB的周长为8cm,则AB=8cm.
如图所示,已知在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB于点E,△DEB的周长为8cm,则AB=8cm. 分析 利用角的平分线上的点到角的两边的距离相等可知Rt△ACD≌Rt△AED,再找出图中的三条等边,利用边的和差关系求AB的长度.
解答 解:∵∠C=90°,DE⊥AB,AD平分∠CAB,
∴CD=DE.
在Rt△ACD与Rt△AED,
$\left\{\begin{array}{l}{CD=DE}\\{AD=AD}\end{array}\right.$,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,
∴BD+DE=BD+CD=BC.
又∵AC=BC,
∴AE=BC,
∴△BDE的周长=BD+DE+BE=AE+BE=8cm,
∴AB=8cm.
故答案为:8cm.
点评 本题主要考查角平分线上的点到线段两端的距离相等的性质和边的和差关系.利用相等的线段进行等效转移是很重要的方法,在角平分线这部分题中常常用到,注意掌握.


科目:初中数学 来源: 题型:解答题
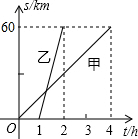 A,B两地相距60km.甲、乙二人分别骑自行车和摩托车沿相同路线匀速行驶,由A地到达B地,他们行驶的路程s(km)与甲出发后的时间t(h)之间的函数图象如图所示
A,B两地相距60km.甲、乙二人分别骑自行车和摩托车沿相同路线匀速行驶,由A地到达B地,他们行驶的路程s(km)与甲出发后的时间t(h)之间的函数图象如图所示查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
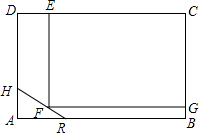 为实现城市绿化,某房地产公司要在拆迁地矩形ABCD(如图)上规划出一块矩形公园CEFG,但不能超过文物保护区△AHR的红线HR.已知AB=210cm,AD=140cm,AR=60cm,AH=40cm,那么当边CE多长时才能使公园CEFG占地面积最大?并求出最大面积.
为实现城市绿化,某房地产公司要在拆迁地矩形ABCD(如图)上规划出一块矩形公园CEFG,但不能超过文物保护区△AHR的红线HR.已知AB=210cm,AD=140cm,AR=60cm,AH=40cm,那么当边CE多长时才能使公园CEFG占地面积最大?并求出最大面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
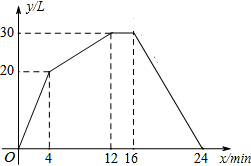 一蓄水池每单位时间内的进、出水量都是一定的,设某时刻开始只进水,不出水,随后既进水又出水,然后既不进水,也不出水,最后只出水不进水,直到将水池中的水放尽,蓄水池中的水量y(L)与时间x(min)之间的关系如图.根据图象解决下列问题:
一蓄水池每单位时间内的进、出水量都是一定的,设某时刻开始只进水,不出水,随后既进水又出水,然后既不进水,也不出水,最后只出水不进水,直到将水池中的水放尽,蓄水池中的水量y(L)与时间x(min)之间的关系如图.根据图象解决下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com