
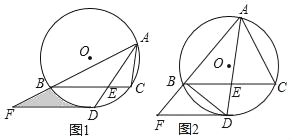
【题目】如图1,△ABC内接于⊙O,∠BAC的平分线交⊙O于点D,交BC于点E(BE>EC),且BD=2![]() .过点D作DF∥BC,交AB的延长线于点F.
.过点D作DF∥BC,交AB的延长线于点F.
(1)求证:DF为⊙O的切线;
(2)若∠BAC=60°,DE=![]() ,求图中阴影部分的面积;
,求图中阴影部分的面积;
(3)若![]() ,DF+BF=8,如图2,求BF的长.
,DF+BF=8,如图2,求BF的长.
【答案】(1)证明见解析(2)9![]() ﹣2π;(3)3
﹣2π;(3)3
【解析】试题分析:(1)连结OD,如图1,由已知得到∠BAD=∠CAD,得到![]() ,再由垂径定理得OD⊥BC,由于BC∥EF,则OD⊥DF,于是可得结论;
,再由垂径定理得OD⊥BC,由于BC∥EF,则OD⊥DF,于是可得结论;
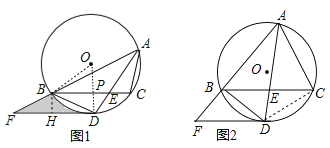
(2)连结OB,OD交BC于P,作BH⊥DF于H,如图1,先证明△OBD为等边三角形得到∠ODB=60°,OB=BD=![]() ,得到∠BDF=∠DBP=30°,在Rt△DBP中得到PD=
,得到∠BDF=∠DBP=30°,在Rt△DBP中得到PD=![]() ,PB=3,在Rt△DEP中利用勾股定理可算出PE=2,由于OP⊥BC,则BP=CP=3,得到CE=1,由△BDE∽△ACE,得到AE的长,再证明△ABE∽△AFD,可得DF=12,最后利用S阴影部分=S△BDF﹣S弓形BD=S△BDF﹣(S扇形BOD﹣S△BOD)进行计算;
,PB=3,在Rt△DEP中利用勾股定理可算出PE=2,由于OP⊥BC,则BP=CP=3,得到CE=1,由△BDE∽△ACE,得到AE的长,再证明△ABE∽△AFD,可得DF=12,最后利用S阴影部分=S△BDF﹣S弓形BD=S△BDF﹣(S扇形BOD﹣S△BOD)进行计算;
(3)连结CD,如图2,由![]() 可设AB=4x,AC=3x,设BF=y,由
可设AB=4x,AC=3x,设BF=y,由![]() 得到CD=BD=
得到CD=BD=![]() ,由△BFD∽△CDA,得到xy=4,再由△FDB∽△FAD,得到16﹣4y=xy,则16﹣4y=4,然后解方程即可得到BF=3.
,由△BFD∽△CDA,得到xy=4,再由△FDB∽△FAD,得到16﹣4y=xy,则16﹣4y=4,然后解方程即可得到BF=3.
试题解析:(1)连结OD,如图1,∵AD平分∠BAC交⊙O于D,∴∠BAD=∠CAD,∴![]() ,∴OD⊥BC,∵BC∥EF,∴OD⊥DF,∴DF为⊙O的切线;
,∴OD⊥BC,∵BC∥EF,∴OD⊥DF,∴DF为⊙O的切线;
(2)连结OB,连结OD交BC于P,作BH⊥DF于H,如图1,∵∠BAC=60°,AD平分∠BAC,∴∠BAD=30°,∴∠BOD=2∠BAD=60°,∴△OBD为等边三角形,∴∠ODB=60°,OB=BD=![]() ,∴∠BDF=30°,∵BC∥DF,∴∠DBP=30°,在Rt△DBP中,PD=
,∴∠BDF=30°,∵BC∥DF,∴∠DBP=30°,在Rt△DBP中,PD=![]() BD=
BD=![]() ,PB=
,PB=![]() PD=3,在Rt△DEP中,∵PD=
PD=3,在Rt△DEP中,∵PD=![]() ,DE=
,DE=![]() ,∴PE=
,∴PE=![]() =2,∵OP⊥BC,∴BP=CP=3,∴CE=3﹣2=1,易证得△BDE∽△ACE,∴AE:BE=CE:DE,即AE:5=1:
=2,∵OP⊥BC,∴BP=CP=3,∴CE=3﹣2=1,易证得△BDE∽△ACE,∴AE:BE=CE:DE,即AE:5=1: ![]() ,∴AE=
,∴AE=![]() ,∵BE∥DF,∴△ABE∽△AFD,∴
,∵BE∥DF,∴△ABE∽△AFD,∴![]() ,即
,即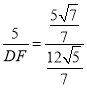 ,解得DF=12,在Rt△BDH中,BH=
,解得DF=12,在Rt△BDH中,BH=![]() BD=
BD=![]() ,∴S阴影部分=S△BDF﹣S弓形BD=S△BDF﹣(S扇形BOD﹣S△BOD)=
,∴S阴影部分=S△BDF﹣S弓形BD=S△BDF﹣(S扇形BOD﹣S△BOD)=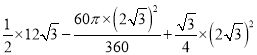 =
=![]() ;
;
(3)连结CD,如图2,由![]() 可设AB=4x,AC=3x,设BF=y,∵
可设AB=4x,AC=3x,设BF=y,∵![]() ,∴CD=BD=
,∴CD=BD=![]() ,∵∠F=∠ABC=∠ADC,∵∠FDB=∠DBC=∠DAC,∴△BFD∽△CDA,∴
,∵∠F=∠ABC=∠ADC,∵∠FDB=∠DBC=∠DAC,∴△BFD∽△CDA,∴![]() ,即
,即![]() ,∴xy=4,∵∠FDB=∠DBC=∠DAC=∠FAD,而∠DFB=∠AFD,∴△FDB∽△FAD,∴
,∴xy=4,∵∠FDB=∠DBC=∠DAC=∠FAD,而∠DFB=∠AFD,∴△FDB∽△FAD,∴![]() ,即
,即![]() ,整理得16﹣4y=xy,∴16﹣4y=4,解得y=3,即BF的长为3.
,整理得16﹣4y=xy,∴16﹣4y=4,解得y=3,即BF的长为3.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】立定跳远是体育中考选考项目之一,体育课上老师记录了某同学的一组立定跳远成绩如表:
成绩(m) | 2.3 | 2.4 | 2.5 | 2.4 | 2.4 |
则下列关于这组数据的说法,正确的是( )
A.众数是2.3B.平均数是2.4
C.中位数是2.5D.方差是0.01
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五四”青年节期间,校团委对团员参加活动情况进行表彰,计划分为优秀奖和贡献奖,为此联系印刷公司设计了两种奖状,A,B两家公司都为学校提出了相同规格和单价的两种奖状,其中优秀奖的奖状6元/张,贡献奖的奖状5元/张,经过协商,A公司的优惠条件是:两种奖状都打八折,但要收制版费50元;B公司的优惠条件是:两种奖状都打九折;根据学校要求,优秀奖的个数是贡献奖的2倍还多10个,如果设贡献奖的个数是x个.
(1)分别写出校团委购买A,B两家印刷厂所需要的总费用y1(元)和y2(元)与贡献奖个数x之间的函数关系式;
(2)校团委选择哪家印刷公司比较合算?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
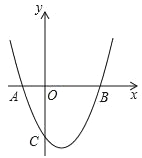
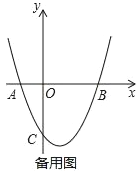
【题目】在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴交于点A,B(A在B的左侧),抛物线的对称轴为直线x=1,AB=4.
(1)求抛物线的表达式;
(2)抛物线上有两点M(x1,y1)和N(x2,y2),若x1<1,x2>1,x1+x2>2,试判断y1与y2的大小,并说明理由;
(3)平移该抛物线,使平移后的抛物线经过点O,且与x轴交于点D,记平移后的抛物线顶点为点P
①若△ODP是等腰直角三角形,求点P的坐标;
②在①的条件下,直线x=m(0<m<3)分别交线段BP、BC于点E、F,且△BEF的面积:△BPC的面积=2:3,直接写出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题再现:
数形结合是一种重要的数学思想方法,借助这种思想方法可将抽象的数学知识变得直观并且具有可操作性.初中数学里的一些代数公式,很多都可以通过表示几何图形面积的方法进行直观推导和解释.
例如:利用图形的几何意义验证完全平方公式.
将一个边长为![]() 的正方形的边长增加
的正方形的边长增加![]() ,形成两个长方形和两个正方形,如图所示:这个图形的面积可以表示成:
,形成两个长方形和两个正方形,如图所示:这个图形的面积可以表示成:
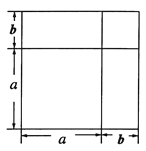
![]() 或
或![]()
∴![]()
这就验证了两数和的完全平方公式.
类比解决:
请你类比上述方法,利用图形的几何意义验证平方差公式.
(要求画出图形并写出推理过程)
问题提出:如何利用图形几何意义的方法证明![]() ?
?
如图所示,![]() 表示1个1×1的正方形,即:
表示1个1×1的正方形,即:![]() ,
,![]() 表示1个2×2的正方形,
表示1个2×2的正方形,![]() 与
与![]() 恰好可以拼成1个2×2的正方形,因此:
恰好可以拼成1个2×2的正方形,因此:![]() 、
、![]() 、
、![]() 就可以表示2个2×2的正方形,即:
就可以表示2个2×2的正方形,即:![]() 而
而![]() 、
、![]() 、
、![]() 、
、![]() 恰好可以拼成一个
恰好可以拼成一个![]() 的大正方形.
的大正方形.
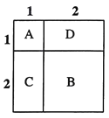
由此可得:![]() .
.
尝试解决:
请你类比上述推导过程,利用图形的几何意义确定:![]() _______.(要求写出结论并构造图形写出推证过程).
_______.(要求写出结论并构造图形写出推证过程).
问题拓广:
请用上面的表示几何图形面积的方法探究:![]() _______.(直接写出结论即可,不必写出解题过程).
_______.(直接写出结论即可,不必写出解题过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y1=k1x+b的图象与x轴、y轴分别交于A、B两点,与反比例函数![]() 的图象分别交于C、D两点,点D(2,﹣3),点B是线段AD的中点.
的图象分别交于C、D两点,点D(2,﹣3),点B是线段AD的中点.
(1)求一次函数y1=k1x+b与反比例函数![]() 的解析式;
的解析式;
(2)求△COD的面积;
(3)直接写出y1>y2时自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于![]() 的不等式组
的不等式组![]() 的整数解仅有
的整数解仅有![]() ,
,![]() ,那么适合这个不等式组的整数
,那么适合这个不等式组的整数![]() ,
,![]() 组成的有序数对
组成的有序数对![]() 共有_______个;如果关于
共有_______个;如果关于![]() 的不等式组
的不等式组![]() (其中
(其中![]() ,
,![]() 为正整数)的整数解仅有
为正整数)的整数解仅有![]() ,那么适合这个不等式组的整数
,那么适合这个不等式组的整数![]() ,
,![]() 组成的有序数对
组成的有序数对![]() 共有______个.(请用含
共有______个.(请用含![]() 、
、![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com