
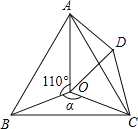
【题目】如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,连接OD.
(1)求证:△OCD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)△AOD能否为等边三角形?为什么?
(4)探究:当α为多少度时,△AOD是等腰三角形.
【答案】(1)、证明过程见解析;(2)、直角三角形、理由见解析;(3)、不能,理由见解析;(4)、α=110°或125°或140°
【解析】
试题分析:(1)、根据△BOC≌△ADC得到OC=DC,结合∠OCD=60°,从而得出等边三角形;(2)、根据△BOC≌△ADC,∠α=150°得到∠ADC=∠BOC=150°,根据等边三角形得到∠ODC=60°,从而得出∠ADO=90°,从而得到三角形的形状;(3)、由△BOC≌△ADC,得∠ADC=∠BOC=∠α,当△AOD为等边三角形时,则∠ADO=60°,结合∠ODC=60°得出∠ADC=120°,又根据∠AOD=∠DOC=60°得出∠AOC=120°,从而求出∠AOC+∠AOB+∠BOC≠360°,从而得到答案;(4)、根据△OCD是等边三角形得到∠COD=∠ODC=60°,根据三角形的性质得出∠ADC=∠BOC=α,∠AOD=190°-α,∠OAD=50°,然后分三种情况分别求出α的大小.
试题解析:(1)、∵△BOC≌△ADC,∴OC=DC.∵∠OCD=60°,∴△OCD是等边三角形.
(2)、△AOD是Rt△.理由如下:
∵△OCD是等边三角形,∴∠ODC=60°, ∵△BOC≌△ADC,∠α=150°,∴∠ADC=∠BOC=∠α=150°,
∴∠ADO=∠ADC-∠ODC=150°-60°=90°,∴△AOD是Rt△.
(3)、不能.理由:由△BOC≌△ADC,得∠ADC=∠BOC=∠α.
若△AOD为等边三角形,则∠ADO=60°,又∠ODC=60°,∴∠ADC=∠α=120°.
又∠AOD=∠DOC=60°,∴∠AOC=120°,又∵∠AOB=110°,
∴∠AOC+∠AOB+∠BOC=120°+120°+110°=350°<360°. 所以△AOD不可能为等边三角形.
(4)、∵△OCD是等边三角形,∴∠COD=∠ODC=60°. ∵∠AOB=110°,∠ADC=∠BOC=α,
∴∠AOD=360°-∠AOB-∠BOC-∠COD=360°-110°-α-60°=190°-α, ∠ADO=∠ADC-∠ODC=α-60°,
∴∠OAD=180°-∠AOD-∠ADO=180°-(190°-α)-(α-60°)=50°.
①当∠AOD=∠ADO时,190°-α=α-60°,∴α=125°.
②当∠AOD=∠OAD时,190°-α=50°,∴α=140°.
③当∠ADO=∠OAD时,α-60°=50°,∴α=110°.
综上所述:当α=110°或125°或140°时,△AOD是等腰三角形.


科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2,直线l3和直线l1,l2交于点C和D,直线l3上有一点P。
(1)如图1,若P点在C,D之间运动时,问∠PAC,∠APB,∠PBD之间的关系是否发生变化,并说明理由;
(2)若点P在C,D两点的外侧运动时(P点与点C,D不重合,如图2和3),试写出∠PAC,∠APB,∠PBD之间的关系,并说明理由。(图3只写结论,不写理由)



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一组数据:5,15,75,45,25,75,45,35,45,35,那么40是这一组数据的( )
A. 平均数但不是中位数 B. 平均数也是中位数
C. 众数 D. 中位数但不是平均数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】沿着一条公路栽树,第一棵栽在路的始端,以后每隔50米栽一棵,要求路的末端栽一棵,这样,缺少21棵树;如果每隔55米栽一棵,要求在路的末端栽一棵,这样,只缺少一棵树.求树的棵数和这条公路的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N.其顶点为D.
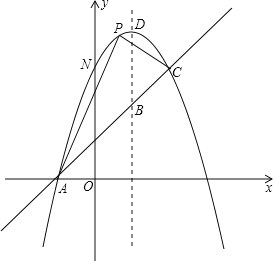
(1)抛物线及直线AC的函数关系式;
(2)设点M(3,m),求使MN+MD的值最小时m的值;
(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;
(4)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com