
【题目】如图,已知直线l1∥l2,直线l3和直线l1,l2交于点C和D,直线l3上有一点P。
(1)如图1,若P点在C,D之间运动时,问∠PAC,∠APB,∠PBD之间的关系是否发生变化,并说明理由;
(2)若点P在C,D两点的外侧运动时(P点与点C,D不重合,如图2和3),试写出∠PAC,∠APB,∠PBD之间的关系,并说明理由。(图3只写结论,不写理由)



【答案】(1)当P点在C、D之间运动时,∠APB=∠PAC+∠PBD(2)当点P在C、D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB.(3)∠PAC=∠PBD+∠APB
【解析】分析:(1)当P点在C、D之间运动时,首先过点P作,由,可得,根据两直线平行,内错角相等,即可求得:∠APB=∠PAC+∠PBD;
(2)当点P在C、D两点的外侧运动时,由直线,根据两直线平行,同位角相等与三角形外角的性质,即可求得: ∠PBD=∠PAC+∠APB.
本题解析: 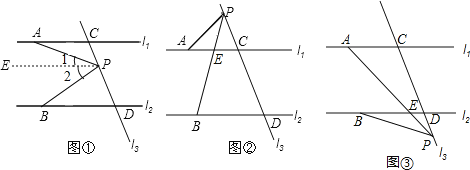
(1)如图①,当P点在C、D之间运动时,∠APB=∠PAC+∠PBD.
理由如下:
过点P作PE∥l1,
∵l1∥l2,
∴PE∥l2∥l1,
∴∠PAC=∠1,∠PBD=∠2,
∴∠APB=∠1+∠2=∠PAC+∠PBD;
(2)如图②,当点P在C、D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB.
理由如下:
∵l1∥l2,
∴∠PEC=∠PBD,
∵∠PEC=∠PAC+∠APB,
∴∠PBD=∠PAC+∠APB.
(3)如图(3),当点P在C、D两点的外侧运动,且在![]() 下方时,∠PAC=∠PBD+∠APB.
下方时,∠PAC=∠PBD+∠APB.
理由如下:理由如下:
∵![]() ∥
∥![]() ,
,
∴∠PED=∠PAC,
∵∠PED=∠PBD+∠APB,
∴∠PAC=∠PBD+∠APB.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
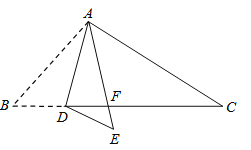
【题目】(本题8分)如图,在△ABC中,D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
(1)求∠AFC的度数;
(2)求∠EDF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人将1 000元人民币按一年期存入银行,一年后本金和利息共获1 018元,利息已扣除20%利息税,则这种存款的利率是( )
A. 1% B. 2% C. 2.25% D. 10%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(1)求一次函数与反比例函数的解析式;
(2)求两函数图象的另一个交点坐标;
(3)直接写出不等式;kx+b≤![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
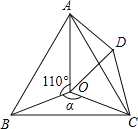
【题目】如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,连接OD.
(1)求证:△OCD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)△AOD能否为等边三角形?为什么?
(4)探究:当α为多少度时,△AOD是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:ABCD的两边AB,AD的长是关于x的方程x2﹣mx+![]() ﹣
﹣![]() =0的两个实数根.
=0的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么ABCD的周长是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com