
����Ŀ����ͼ��ƽ��ֱ������ϵ�У����� OABC �� �� �� A��0��3����C��- 1��0��. �� �� �� OABC ��ԭ��˳ʱ����ת 900���õ����� OA��B��C��.����������⣺
��1�����ֱ�� BB���ĺ�������ʽ��
��2��ֱ�� BB���� x �ύ�ڵ� M���� y �ύ�ڵ�N�������� y = ax2+ bx + c ��ͼ����C��M��N���������ߵĺ�������ʽ.
��3������MON ��ֱ�� MN ���ۣ��� O ���ڵ�P ���������жϵ� P �Ƿ����������ϣ�˵������.

���𰸡���1��y=-![]() ;(2)y=
;(2)y=![]() ;(3)����.
;(3)����.
��������������������⿼����κ������ۺ�Ӧ�ã������漰����֪ʶ���д���ϵ������������ʽ�ͺ���ͼ���ϵ�����壬���ε�����������������ͷ���֮��Ĺ�ϵ�ȣ�Ҫ�������ղ���������ã�
��1�������ı���OABC�Ǿ��ο�֪B��-1��3����������ת�����ʣ���B����3��1����
��B��-1��3����B����3��1������y=mx+n�У����ô���ϵ�����ɽ��y=-![]() ��
��
��2���ɣ�1���ã�N��0��![]() ����M��5��0��������κ�������ʽΪy=a
����M��5��0��������κ�������ʽΪy=a![]() +bx+c����C��-1��0����M��5��0����N��0��
+bx+c����C��-1��0����M��5��0����N��0��![]() ������ã����ô���ϵ������ö��κ�������ʽΪy=
������ã����ô���ϵ������ö��κ�������ʽΪy=![]()
![]() +2x+
+2x+![]() ��
��
��3������O��OD��MN�ڵ�D����M��N������꣬�����ON��OM��ֵ���������MN��ֵ��Ȼ������OD��ֵ���������OP��ֵ���õ�P������꣬Ȼ��P���������������ߵĽ���ʽ�������жϵ�P�Ƿ����������ϣ�
�����������1��������ã�B��![]() ��3����
��3����![]() ��3��1����
��3��1����
��ֱ��![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ��
��
��2��ֱ��![]() ��
��![]() ��Ľ���ΪM��5��0����
��Ľ���ΪM��5��0����
��![]() ��Ľ���N��0��
��Ľ���N��0��![]() ����
����
�������ߵĽ���ʽΪ![]() ��
��
�������߹���N��
��![]() ��
��
��![]() ��
��
�������ߵĽ���ʽΪ![]() =
=![]() ��
��
��3������O��OD��MN�ڵ�D��
��M��5��0����N��0��![]() ����
����
��ON=![]() ��OM=5��
��OM=5��
��MN=![]() ��
��
��OD=![]() ��
��
������MON��ֱ��MN���ۣ���O���ڵ�P����
��OP=![]() ��
��
��P��2��4�����������ߵĽ���ʽ��
��P�����������ϣ�


 ���������ּ���ÿһ��ȫ�º�����ҵ��ϵ�д�
���������ּ���ÿһ��ȫ�º�����ҵ��ϵ�д� ��ٽ������½������������ϵ�д�
��ٽ������½������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��֪��ǡ�AOB������OC����OA��OB�غϣ�OM��ON�ֱ�ƽ�֡�AOC����BOC.

(1)��OC�ڡ�AOB���ڲ�
������BOC=50������AOC=20�������MON�Ĵ�С��
������MON=30�������AOB�Ĵ�С��
(2)������OC�ڡ�AOB�ⲿ���ҡ�AOB=80������ֱ��д����MON�Ĵ�С.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ˮ��ɽ���ǽ�ɽ��ɽ�����ҳ���ȫ��ֲ�����ڽ���3��12��ֲ���ڵ��죬ijУ���꼶һ��48��ѧ��ȫ���μ���ֲ���������ÿ������4�꣬Ů��ÿ������3�꣬ȫ�����170�ꡣ
��1���ð��С�Ů����Ϊ�����ˣ�
��2��ѧУѡ����ס����������磬������![]() ��������
��������![]() .���Ҫʹ���������Ǯ������1200Ԫ����ô�����Թ������������ꣿ
.���Ҫʹ���������Ǯ������1200Ԫ����ô�����Թ������������ꣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AOΪRt��ABC�Ľ�ƽ���ߣ���ACB=90�㣬![]() ����OΪԲ�ģ�OC Ϊ�뾶��Բ�ֱ�AO��BC�ڵ�D��E������ED���ӳ���AC�ڵ�F��
����OΪԲ�ģ�OC Ϊ�뾶��Բ�ֱ�AO��BC�ڵ�D��E������ED���ӳ���AC�ڵ�F��
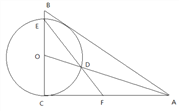
��1����֤��AB�ǡ�O�����ߣ�
��2����![]() ��ֵ��
��ֵ��
��3������O�İ뾶Ϊ4����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ���� C ���� AB Ϊֱ���ġ�O �ϣ��� D �� AB ���ӳ����ϣ���BCD =��A.
��1����֤��CD Ϊ��O �����ߣ�
��2������ C �� CE��AB �ڵ� E.�� CE = 2��cos D =![]() ���� AD �ij�.
���� AD �ij�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾����Ʒ���ع���ij������ˮ��ο��ҽ�����ߣ���Ʒ���ضԹ�������3000kg���ϣ���3000kg���Ĺ˿Ͳ����������۷���.������ÿǧ��9Ԫ���ɻ����ͻ����ţ��ҷ�����ÿǧ��8Ԫ���ɹ˿��Լ���˻�.��֪�ù�˾��ӻ��ص���˾���������Ϊ5000Ԫ.
��1���ֱ�д���ù�˾���ֹ���������y��Ԫ�����������ˮ����x��kg��֮��ĺ�����ϵʽ.
��2��������������һ��Χʱ��ѡ�����ֹ����������٣���˵������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪x1��x2��һԪ���η��̣�a��6��x2+2ax+a=0������ʵ������
��1���Ƿ����ʵ��a��ʹ��x1+x1x2=4+x2�����������ڣ����a��ֵ���������ڣ�����˵�����ɣ�
��2����ʹ��x1+1����x2+1��Ϊ��������ʵ��a������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У��߳�Ϊ2�ĵȱ�������AEF�Ķ���E��F�ֱ���BC��CD�ϣ����н��ۣ���BE=DF���ڡ�AEB=75������CE=2����S������ABCD=2+![]() ��������ȷ���ǣ�������
��������ȷ���ǣ�������

A.�٢�B.�ڢ�C.�٢ڢ�D.�٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����0 ΪRt��ABCб��AB�ϵ�һ�㣬��OA Ϊ�뾶�Ĩ�O��BC���ڵ�D����AC ���ڵ�E,����AD.
(1) ��֤: ADƽ�֡�BAC;
(2)����BAC= 60��,OA=4,����Ӱ���ֵ����(���������).
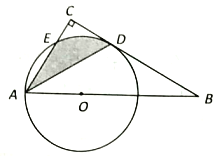
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com