练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某公司到果品基地购买某种优质水果慰问医务工作者，果品基地对购买量在3000kg以上（含3000kg）的顾客采用两种销售方案.甲方案：每千克9元，由基地送货上门；乙方案：每千克8元，由顾客自己租车运回.已知该公司租车从基地到公司的运输费用为5000元.

    （1）分别写出该公司两种购买方案付款金额y（元）与所购买的水果量x（kg）之间的函数关系式.

    （2）当购买量在哪一范围时，选择哪种购买方案付款最少？并说明理由

    【答案】（1）；；（2）详见解析

    【解析】

    (1)甲方案的付款=甲水果单价x购买量,乙方案的付款=乙水果单价x购买量+运输费,根据这两个关系分别列式即可;
    (2)将甲和乙的两种方案所需的付款数进行比较,从而确定购买量的范围.

    （1）；；
    (2)当时,即,
    解得.

    当 kg时,两种付款一样.
    当y甲<y乙时,有

    解得.
    当时,选择甲种方案付款少.
    当y甲>y乙时,有,
    当 kg时,选择乙种方案付款少.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】现有正方形ABCD和一个以O为直角顶点的三角板，移动三角板，使三角板的两直角边所在直线分别与直线BC，CD交于点M，N．

    （1）如图1，若点O与点A重合，则OM与ON的数量关系是__________________；

    （2）如图2，若点O在正方形的中心（即两对角线的交点），则（1）中的结论是否仍然成立？请说明理由；

    （3）如图3，若点O在正方形的内部（含边界），当OM=ON时，请探究点O在移动过程中可形成什么图形？

    （4）如图4是点O在正方形外部的一种情况．当OM=ON时，请你就“点O的位置在各种情况下（含外部）移动所形成的图形”提出一个正确的结论．（不必说理）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

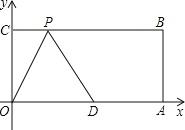
    【题目】已知，如图：在平面直角坐标系中，O为坐标原点，四边形OABC是矩形，点A、C的坐标分别为、，点D是OA的中点，点P在BC边上运动，当是等腰三角形时，点Р的坐标为_______________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：如图1，点把线段分割成,若以为边的三角形是一个直角三角形，则称是线段的勾股点。

    (1)已知点是线段的勾股点，若,求的长。

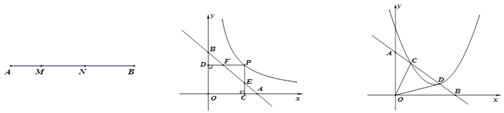
    (图1) （图2） （图3）

    (2)如图2，点是反比例函数上的动点，直线与坐标轴分别交与两点，过点分别向轴作垂线，垂足为，且交线段于。试证明：是线段的勾股点。

    (3)如图3，已知一次函数与坐标轴交与两点，与二次函数交与两点，若是线段的勾股点，求的值。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，平面直角坐标系中，矩形 OABC 的 顶 点 A（0，3），C（- 1，0）. 将 矩 形 OABC 绕原点顺时针旋转 900，得到矩形 OA’B’C’.解答下列问题：

    （1）求出直线 BB’的函数解析式；

    （2）直线 BB’与 x 轴交于点 M、与 y 轴交于点N，抛物线 y = ax2+ bx + c 的图象经过点C、M、N，求抛物线的函数解析式.

    （3）将△MON 沿直线 MN 翻折，点 O 落在点P 处，请你判断点 P 是否在抛物线上，说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

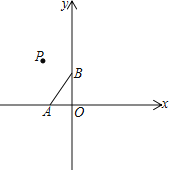
    【题目】已知：平面直角坐标系中，点A(－2，0)、B(0，3)，点P为第二象限内一点

    (1) 如图，将线段AB绕点P旋转180°得线段CD，点A与点C对应，试画出图形；

    (2) 若(1)中得到的点C、D恰好在同一个反比例函数的图象上，试求直线BC的解析式；

    (3) 若点Q(m，n)为第四象限的一点，将线段AB绕点Q顺时针旋转90°到点E、F．若点E、F恰好在同一个反比例函数的图象上，试直接写出m、n之间的关系式__________________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A（﹣3，2），B（0，4），C（0，2）．

    （1）将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△A1B1C；

    （2）平移△ABC，若点A的对应点A2的坐标为（0，﹣4），画出平移后对应的△A2B2C2 ；

    （3）若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标 .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，AB＝4，BC＝5，AF平分∠DAE，EF⊥AE，求CF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，关于x的一元二次方程x2+（1﹣k）x﹣k=0 （其中k为常数）．

    （1）判断方程根的情况并说明理由；

    （2）若﹣1＜k＜0，设方程的两根分别为m，n（m＜n），求它的两个根m和n；

    （3）在（2）的条件下，若直线y=kx﹣1与x轴交于点C，x轴上另两点A（m，0）、点B（n，0），试说明是否存在k的值，使这三点中相邻两点之间的距离相等？若存在，求出k的值；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案