
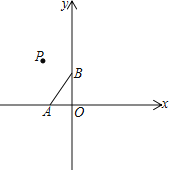
����Ŀ����֪��ƽ��ֱ������ϵ�У���A(��2��0)��B(0��3)����PΪ�ڶ�������һ��
(1) ��ͼ�����߶�AB�Ƶ�P��ת180�����߶�CD����A���C��Ӧ���Ի���ͼ����
(2) ��(1)�еõ��ĵ�C��Dǡ����ͬһ������������![]() ��ͼ���ϣ�����ֱ��BC�Ľ���ʽ��
��ͼ���ϣ�����ֱ��BC�Ľ���ʽ��
(3) ����Q(m��n)Ϊ��������һ�㣬���߶�AB�Ƶ�Q˳ʱ����ת90������E��F������E��Fǡ����ͬһ��������������ͼ���ϣ���ֱ��д��m��n֮��Ĺ�ϵʽ__________________��
���𰸡�m����5n
��������������(1)�ҳ���A,B���ڵ�P�ĶԳƵ㣬���Ӽ���.
![]() ��P(m��n)����C(2��2m��2n)��D(2m��2n��3)�����ݵ�C��Dǡ����ͬһ������������
��P(m��n)����C(2��2m��2n)��D(2m��2n��3)�����ݵ�C��Dǡ����ͬһ������������![]() ��ͼ���ϣ���2n(2��2m)��2m(2n��3)���õ�2n��-3m����ֱ��BC�Ľ���ʽΪ��y��kx��3������C(2��2m��-3m)����y��kx��3���������һ�κ�������ʽ.
��ͼ���ϣ���2n(2��2m)��2m(2n��3)���õ�2n��-3m����ֱ��BC�Ľ���ʽΪ��y��kx��3������C(2��2m��-3m)����y��kx��3���������һ�κ�������ʽ.
![]() ������ת���������E(m��n��m��n��2)��F(m��3��n��n��m),����
������ת���������E(m��n��m��n��2)��F(m��3��n��n��m),����![]() �������m��n֮��Ĺ�ϵʽ.
�������m��n֮��Ĺ�ϵʽ.
��⣺(1)��ͼ��ʾ��
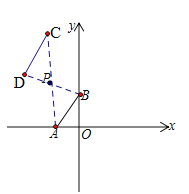
(2) ��P(m��n)����C(2��2m��2n)��D(2m��2n��3)
�ߵ�C��Dǡ����ͬһ������������![]() ��ͼ����
��ͼ����
��2n(2��2m)��2m(2n��3)����2n��-3m��
��ֱ��BC�Ľ���ʽΪ��y��kx��3
��C(2��2m����3m)����y��kx��3����
![]() �����
�����![]() ��
��![]()
(3) ������ֱ�ã�E(m��n��m��n��2)��F(m��3��n��n��m)
��(m��n)(m��n��2)��(m��3��n)(n��m)��
������m��-5n.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
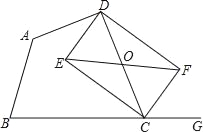
����Ŀ����֪����ͼ�����ı���ABCD�У���G�ڱ�BC���ӳ����ϣ�CEƽ����BCD��CFƽ����GCD��EF��BC��CD�ڵ�O��
��1����֤��OE=OF��
��2������OΪCD���е㣬��֤���ı���DECF�Ǿ��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽ⱾУ���꼶ѧ����ĩ��ѧ����������ھ��꼶�����ȡ��һ����ѧ�� ����ĩ��ѧ�ɼ�Ϊ��������Ϊ A��90��100 �֣���B��80��89 �֣���C��60��79 �֣���D��0��59 �֣��ĸ��ȼ�����ͳ�ƣ�����ͳ�ƽ�����Ƴ�����ͳ��ͼ���������ͳ��ͼ������� ����.
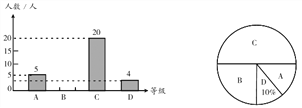
��1����������ȡ��ѧ�����ж����ˣ�
��2���벹ȫ����ͳ��ͼ��
��3�����ѧУ���꼶����ѧ�� 1200 �ˣ�������Ϊ 80 �֣��� 80 �֣�����Ϊ���㣬��� ����ξ��꼶ѧ����ĩ��ѧ���Գɼ�Ϊ�����ѧ��������Լ�ж��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����⣺�Ķ����в��ϣ���֪��������ʽ2x2+x+a��һ����ʽ�ǣ�x+2��������һ����ʽ�Լ�a ��ֵ
�⣺����һ����ʽ�ǣ�2x+b����
�������⣬��2x2+x+a=(x+2)(2x+b)��
չ������2x2+x+a =2x2+(b+4)x+2b��
����![]() �����
�����![]() ��
��
���ԣ���һ����ʽ�ǣ�2x3����a ��ֵ��6.
���������������������⣺��֪��������ʽ3x2 10x m ��һ����ʽ�ǣ�x+4��������һ����ʽ�Լ�m��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾����Ʒ���ع���ij������ˮ��ο��ҽ�����ߣ���Ʒ���ضԹ�������3000kg���ϣ���3000kg���Ĺ˿Ͳ����������۷���.������ÿǧ��9Ԫ���ɻ����ͻ����ţ��ҷ�����ÿǧ��8Ԫ���ɹ˿��Լ���˻�.��֪�ù�˾��ӻ��ص���˾���������Ϊ5000Ԫ.
��1���ֱ�д���ù�˾���ֹ���������y��Ԫ�����������ˮ����x��kg��֮��ĺ�����ϵʽ.
��2��������������һ��Χʱ��ѡ�����ֹ����������٣���˵������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
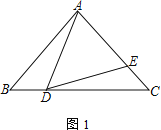
����Ŀ����֪����ABC�У���DΪ��BC��һ�㣬��E�ڱ�AC�ϣ�����ADE����B
(1) ��ͼ1����AB��AC����֤��![]() ��
��
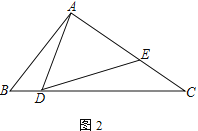
(2) ��ͼ2����AD��AE����֤��![]() ��
��
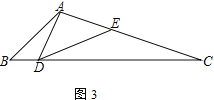
(3) ��(2)�������£�����DAC��90������CE��4��tan��BAD��![]() ����AB��____________��
����AB��____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�κ���y��kx+b��k��b�dz��������Ա���x��ȡֵΪ1��x��5ʱ����Ӧ�ĺ���ֵ�ķ�ΧΪ��2��y��2�����һ�κ����Ľ���ʽΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ������Ӧ�����ﴫͳ�Ļ����ĺ��٣�ijѧУ��֯ȫУ1200��ѧ�����о���ʫ���ж�������ڻ֮��ٰ쾭��ʫ�ʴ�����Ϊ�˽Ȿ��ϵ�л�ij���Ч����ѧУ��ί�ڻ����֮���������ȡ40��ѧ��������һ��ʫ���б������������ݵ��������Ƴɵ�ͳ��ͼ��ͼ��ʾ.

����������һ���£��ٴγ���ⲿ��ѧ����һ��ʫ���б������������Ƴ�ͳ�Ʊ����£�
һ��ʫ���б����� | 3�� | 4�� | 5�� | 6�� | 7�� | 8�� |
���� | 1 | 3 | 5 | 6 | 10 | 15 |
����ݵ������Ϣ
��1��������֮��ѧ����һ��ʫ���б�����������λ����
��2�����ƴ�����һ���¸�Уѧ��һ��ʫ���б�6�ף���6�ף����ϵ�������
��3��ѡ���ʵ���ͳ���������ٴ�������ͬ�ĽǶȷ������ε����������ݣ����۸�У����ʫ���б�ϵ�л��Ч��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ����в��ϣ�
���⣺��ͼ1���ڵȱ�������ABC����һ��P����PA=2��PB=![]() ��PC=1�����BPC�����Ĵ�С�͵ȱ�������ABC�ı߳���
��PC=1�����BPC�����Ĵ�С�͵ȱ�������ABC�ı߳���
����ͬѧ��˼·�ǣ�����BPC�Ƶ�B��ʱ����ת60����������ת���ͼ�Σ���ͼ2��������PP�����ɵá�P��PC�ǵȱ������Σ�����PP��A����ֱ�������Σ��ɹ��ɶ������涨����֤�����Ӷ��õ���BPC=��AP��B=__________������������ȱߡ�ABC�ı߳�Ϊ__________��
����õ������
����ο�����ͬѧ��˼·��̽��������������⣺��ͼ3����������ABCD����һ��P����PA=![]() ��BP=
��BP=![]() ��PC=1�����BPC�����Ĵ�С��������ABCD�ı߳���
��PC=1�����BPC�����Ĵ�С��������ABCD�ı߳���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com