
【题目】已知,关于x的一元二次方程x2+(1﹣k)x﹣k=0 (其中k为常数).
(1)判断方程根的情况并说明理由;
(2)若﹣1<k<0,设方程的两根分别为m,n(m<n),求它的两个根m和n;
(3)在(2)的条件下,若直线y=kx﹣1与x轴交于点C,x轴上另两点A(m,0)、点B(n,0),试说明是否存在k的值,使这三点中相邻两点之间的距离相等?若存在,求出k的值;若不存在,请说明理由.
【答案】(1) 方程有两个实数根(2) m=k,n=﹣1(3)k=-![]()
【解析】分析:(1)求出判别式的值即可判断.
(2)求出方程的两个根,根据题意即可解决问题.
(3)先求出A、B、C三点坐标,根据题意判断A、B、C的位置,列出方程即可解决问题.
详解:(1)∵△=(1﹣k)2+4k=k2﹣2k+1+4k=k2+2k+1=(k+1)2≥0,∴方程有两个实数根.
(2)∵x2+(1﹣k)x﹣k=0,∴(x﹣k)(x+1)=0,∴x=k或﹣1.
∵﹣1<k<0,设方程的两根分别为m,n(m<n),∴m=k,n=﹣1.
(3)存在.由题意A(k,0),B(﹣1,0),C(![]() ,0).
,0).
∵﹣1<k<0,∴﹣1<k<![]() .
.
∵AC=AB,∴k﹣![]() =1﹣k,整理得:2k2﹣k+1=0,解得:k=﹣
=1﹣k,整理得:2k2﹣k+1=0,解得:k=﹣![]() 或1(舍弃),
或1(舍弃),
∴当k=﹣![]() 时,A、B、C三点中相邻两点之间的距离相等.
时,A、B、C三点中相邻两点之间的距离相等.


科目:初中数学 来源: 题型:
【题目】某公司到果品基地购买某种优质水果慰问医务工作者,果品基地对购买量在3000kg以上(含3000kg)的顾客采用两种销售方案.甲方案:每千克9元,由基地送货上门;乙方案:每千克8元,由顾客自己租车运回.已知该公司租车从基地到公司的运输费用为5000元.
(1)分别写出该公司两种购买方案付款金额y(元)与所购买的水果量x(kg)之间的函数关系式.
(2)当购买量在哪一范围时,选择哪种购买方案付款最少?并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=-x+60(30≤x≤60).
设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1:y=x+n﹣2与直线l2:y=mx+n相交于点P(1,2).
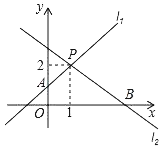
(1)求m,n的值;
(2)请结合图象直接写出不等式mx+n>x+n﹣2的解集.
(3)若直线l1与y轴交于点A,直线l2与x轴交于点B,求四边形PAOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
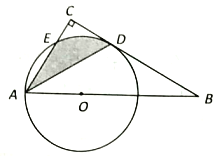
【题目】如图,点0 为Rt△ABC斜边AB上的一点,以OA 为半径的☉O与BC切于点D,与AC 交于点E,连接AD.
(1) 求证: AD平分∠BAC;
(2)若∠BAC= 60°,OA=4,求阴影部分的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
问题:如图1,在等边三角形ABC内有一点P,且PA=2,PB=![]() ,PC=1、求∠BPC度数的大小和等边三角形ABC的边长.
,PC=1、求∠BPC度数的大小和等边三角形ABC的边长.
李明同学的思路是:将△BPC绕点B逆时针旋转60°,画出旋转后的图形(如图2),连接PP′,可得△P′PC是等边三角形,而△PP′A又是直角三角形(由勾股定理的逆定理可证),从而得到∠BPC=∠AP′B=__________;,进而求出等边△ABC的边长为__________;
问题得到解决.
请你参考李明同学的思路,探究并解决下列问题:如图3,在正方形ABCD内有一点P,且PA=![]() ,BP=
,BP=![]() ,PC=1.求∠BPC度数的大小和正方形ABCD的边长.
,PC=1.求∠BPC度数的大小和正方形ABCD的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当﹣2<x<2时,下列函数中,函数值y随自变量x增大而增大的有( )个.
①y=2x;②y=2﹣x;③y=﹣![]() ;④y=x2+6x+8.
;④y=x2+6x+8.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着气温的升高,空调的需求量大增.某家电超市对每台进价分别为2000元、1700元的![]() 、
、![]() 两种型号的空调,近两周的销售情况统计如下:
两种型号的空调,近两周的销售情况统计如下:
销售时段 | 销售量 | 销售收入 | |
|
| ||
第一周 | 6台 | 7台 | 31000元 |
第二周 | 8台 | 11台 | 45000元 |
(1)求![]() 、
、![]() 两种型号的空调的销售价;
两种型号的空调的销售价;
(2)若该家电超市准备用不多于54000元的资金,采购这两种型号的空调30台,求![]() 种型号的空调最多能采购多少台?
种型号的空调最多能采购多少台?
(3)在(2)的条件下,该家电超市售完这30台空调能否实现利润不低于15800元的目标?若能,请给出采购方案.若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,△ABC中,AB=AC,∠A=36°.
(1)作AB边的垂直平分线,垂足为M,交AC于N,连结BN.(不写作法,保留作图痕迹)
(2)①直接写出∠ABN的度数为 ;
②若BC=12,直接写出BN的长为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com