
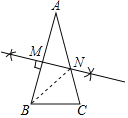
【题目】已知,如图,△ABC中,AB=AC,∠A=36°.
(1)作AB边的垂直平分线,垂足为M,交AC于N,连结BN.(不写作法,保留作图痕迹)
(2)①直接写出∠ABN的度数为 ;
②若BC=12,直接写出BN的长为 .

【答案】(1)详见解析;(2)36°,12.
【解析】
(1)根据题意,根据垂直平分线的画法进行尺规作图即可;
(2)根据垂直平分线上的点到线段两端的距离相等即可得出∠ABN=∠A;
(3)根据垂直平分线的性质和三角形外角定理,可知∠BNC=72°,再根据AB=AC,∠A=36°,得出∠C=72°,可得BC=BN=12.
解:(1)如图所示:MN即为所求;
(2)①∠ABN的度数为:36°;
②∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
∵直线MN垂直平分线AB,
∴AN=BN,
∴∠ABN=∠A=36°,
∴∠CBN=36°,
∴∠BNC=72°,
∴BC=BN=12.
故答案为:36°,12.


科目:初中数学 来源: 题型:
【题目】已知,关于x的一元二次方程x2+(1﹣k)x﹣k=0 (其中k为常数).
(1)判断方程根的情况并说明理由;
(2)若﹣1<k<0,设方程的两根分别为m,n(m<n),求它的两个根m和n;
(3)在(2)的条件下,若直线y=kx﹣1与x轴交于点C,x轴上另两点A(m,0)、点B(n,0),试说明是否存在k的值,使这三点中相邻两点之间的距离相等?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一辆摩拜单车放在水平的地面上,车把头下方A处与坐垫下方B处在平行于地面的水平线上,A、B之间的距离约为49cm,现测得AC、BC与AB的夹角分别为45°与68°,若点C到地面的距离CD为28cm,坐垫中轴E处与点B的距离BE为4cm,求点E到地面的距离(结果保留一位小数).(参考数据:sin68°≈0.93,cos68°≈0.37,cot68°≈0.40)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应绿色出行号召,越来越多市民选择租用共享单车出行,已知某共享单车公司为市民提供了手机支付和会员卡支付两种支付方式,如图描述了两种方式应支付金额y(元)与骑行时间x(时)之间的函数关系,根据图象回答下列问题:
(1)求手机支付金额y(元)与骑行时间x(时)的函数关系式;
(2)李老师经常骑行共享单车,请根据不同的骑行时间帮他确定选择哪种支付方式比较合算.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某小区开展了“节约用水为环保做贡献”的活动,为了解居民用水情况,在小区随机抽查了10户家庭的月用水量,结果如下表
月用水量(吨) | 8 | 9 | 10 |
户数 | 2 | 6 | 2 |
则关于这10户家庭的月用水量,下列说法错误的是 ( )
A. 方差是4 B. 极差2 C. 平均数是9 D. 众数是9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳市某校艺术节期间,开展了“好声音”歌唱比赛,在初赛中,学生处对初赛成绩做了统计分析,绘制成如下频数、频率分布直方图(如图),请你根据图表提供的信息,解答下列问题:
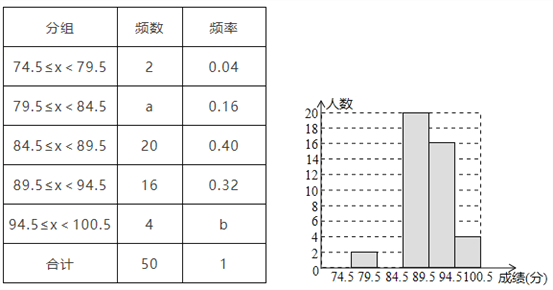
(1)频数、频率分布表中a=_______,b=_______;
(2)补全频数分布直方图;
(3)初赛成绩在94.5≤x<100.5分的四位同学恰好是七年级、八年级各一位,九年级两位,学生处打算从中随机挑选两位同学谈一下决赛前的训练,则所选两位同学恰好都是九年级学生的概率为_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:二元一次方程![]() 有无数组解,每组解记为
有无数组解,每组解记为![]() ,称
,称![]() 为亮点,将这些亮点连接得到一条直线,称这条直线是亮点的隐线,答下列问题:
为亮点,将这些亮点连接得到一条直线,称这条直线是亮点的隐线,答下列问题:
(1) 已知![]() ,则是隐线
,则是隐线![]() 的亮点的是 ;
的亮点的是 ;
(2) 设![]() 是隐线
是隐线![]() 的两个亮点,求方程
的两个亮点,求方程![]() 中
中![]() 的最小的正整数解;
的最小的正整数解;
(3)已知![]() 是实数, 且
是实数, 且![]() ,若
,若![]() 是隐线
是隐线![]() 的一个亮点,求隐线
的一个亮点,求隐线![]() 中的最大值和最小值的和.
中的最大值和最小值的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
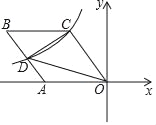
【题目】如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC=![]() ,反比例函数y=﹣
,反比例函数y=﹣![]() 的图象经过点C,与AB交与点D,则△COD的面积的值等于_____;
的图象经过点C,与AB交与点D,则△COD的面积的值等于_____;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com