练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

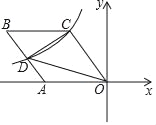
    【题目】如图，菱形OABC的一边OA在x轴的负半轴上，O是坐标原点，tan∠AOC=，反比例函数y=﹣的图象经过点C，与AB交与点D，则△COD的面积的值等于_____；

    【答案】10．

    【解析】分析：易证S菱形ABCO=2S△CDO，再根据tan∠AOC的值，可以假设OF=3x，推出OC=5x，可得OA=OC=5x，S菱形ABCO=AOCF=20x2，由C（﹣3x，4x），可得×3x×4x=6，推出x2=1，由此即可解决问题．

    详解：作DE∥AO，CF⊥AO，设CF=4x，

    ∵四边形OABC为菱形，∴AB∥CO，AO∥BC．

    ∵DE∥AO，∴S△ADO=S△DEO，同理S△BCD=S△CDE．

    ∵S菱形ABCO=S△ADO+S△DEO+S△BCD+S△CDE，∴S菱形ABCO=2（S△DEO+S△CDE）=2S△CDO．

    ∵tan∠AOC=，∴OF=3x，∴OC=5x，∴OA=OC=5x．

    ∵S菱形ABCO=AOCF=20x2．

    ∵C（﹣3x，4x），∴×3x×4x=6，∴x2=1，∴S菱形ABCO=20，∴△COD的面积=10．

    故答案为：10．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知，如图，△ABC中，AB＝AC，∠A＝36°．

    （1）作AB边的垂直平分线，垂足为M，交AC于N，连结BN．（不写作法，保留作图痕迹）

    （2）①直接写出∠ABN的度数为　 　；

    ②若BC＝12，直接写出BN的长为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】蜗牛从某点开始沿一条东西方向的直线爬行，规定以出发点为原点，向东爬行的路程记为正数，向西爬行的路程记为负数，则蜗牛爬过的各段路程依次为+5，－3，+10，－8，－6，+12，－10.（单位：厘米）

    （1）请判断蜗牛最后是否回到出发点？

    （2）蜗牛离开出发点0最远时是多少厘米？

    （3）在爬行过程中，若蜗牛每爬1厘米就奖励一粒芝麻，则蜗牛一共得到多少粒芝麻？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

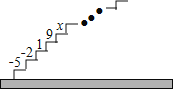
    【题目】如图，阶梯图的每个台阶上都标着一个数，从下到上的第1个至第4个台阶上依次标着﹣5，﹣2，1，9，且任意相邻四个台阶上数的和都相等．

    尝试 （1）求前4个台阶上数的和是多少？

    （2）求第5个台阶上的数x是多少？

    应用 求从下到上前31个台阶上数的和．

    发现 试用含k（k为正整数）的式子表示出数“1”所在的台阶数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了提高学生书写汉字的能力，增强保护汉字的意识，某校举办了“汉字听写大赛”，学生经选拔后进入决赛，测试同时听写100个汉字，每正确听写出一个汉字得1分，本次决赛，学生成绩为（分），且（无满分），将其按分数段分为五组，绘制出以下不完整表格：

    组别

    成绩（分）

    频数（人数）

    频率

    一

    2

    二

    10

    0.2

    三

    12

    四

    0.4

    五

    6

    请根据表格提供的信息，解答以下问题：

    （1）本次决赛共有__________名学生参加；

    （2）直接写出表中：_______________________

    （3）请补全右面相应的频数分布直方图；

    （4）若决赛成绩不低于80分为优秀，则本次大赛的优秀率为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知函数 y =kx2 +(k +1)x +1（k 为实数），

    （1）当 k＝3 时，求此函数图象与 x 轴的交点坐标；

    （2）判断此函数与 x 轴的交点个数，并说明理由；

    （3）当此函数图象为抛物线，且顶点在 x 轴下方，顶点到 y 轴的距离为 2，求 k 的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】今年,在端午节前夕,三位同学到某超市调研一种进价为2元的粽子的销售情况．（售价不低于进价）.请根据小丽提供的信息,解答小华和小明提出的问题．

    认真阅读上面三位同学的对话,请根据小丽提供的信息．

    （1）解答小华的问题；

    （2）解答小明的问题．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校随机选取40名学生进行军运会知识考查，对考查成绩进行统计（成绩均为整数），并依据统计数据绘制了如下统计图表．解答下列问题：

    组别

    分数段/分

    频数

    频率

    1

    50.5~60.5

    2

    a

    2

    60.5~70.5

    6

    0.15

    3

    70.5~80.5

    b

    c

    4

    80.5~90.5

    12

    0.30

    5

    90.5~100.5

    6

    0.15

    合计

    40

    1.00

    (1) 表中a＝______；b＝______；c＝____;

    (2) 请补全频数分布直方图;

    (3) 已知该学校共有学生1280人，若考查成绩80分以上（不含80分）为优秀，试估计该学校学生军运会知识考查成绩达到优秀的人数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】随着通讯技术迅猛发展，人与人之间的沟通方式更多样、便捷．某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷（每人必选且只选一种），在全校范围内随机调查了部分学生，将统计结果绘制了如下两幅不完整的统计图，请结合图中所给的信息解答下列问题：

    （1）这次统计共抽查了　　名学生；在扇形统计图中，表示“QQ”的扇形圆心角的度数为　 　；

    （2）将条形统计图补充完整；

    （3）该校共有1500名学生，请估计该校最喜欢用“微信”进行沟通的学生有多少名？

    （4）某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系，请用列表或画树状图的方法求出甲、乙两名同学恰好选中同一种沟通方式的概率．

    查看答案和解析>>

    同步练习册答案