
【题目】随着气温的升高,空调的需求量大增.某家电超市对每台进价分别为2000元、1700元的![]() 、
、![]() 两种型号的空调,近两周的销售情况统计如下:
两种型号的空调,近两周的销售情况统计如下:
销售时段 | 销售量 | 销售收入 | |
|
| ||
第一周 | 6台 | 7台 | 31000元 |
第二周 | 8台 | 11台 | 45000元 |
(1)求![]() 、
、![]() 两种型号的空调的销售价;
两种型号的空调的销售价;
(2)若该家电超市准备用不多于54000元的资金,采购这两种型号的空调30台,求![]() 种型号的空调最多能采购多少台?
种型号的空调最多能采购多少台?
(3)在(2)的条件下,该家电超市售完这30台空调能否实现利润不低于15800元的目标?若能,请给出采购方案.若不能,请说明理由.
【答案】(1)A、B两种型号空调的销售价分别为2600元和2200元;(2) 10台;(3)见解析.
【解析】
(1)设A、B两种型号电风扇的销售单价分别为x元、y元,根据6台A型号7台B型号的电扇收入31000元,8台A型号11台B型号的电扇收入45000元,列方程组求解即可;
(2)设采购A种型号电风扇a台,则采购B种型号电风扇(30-a)台,根据金额不多余54000元,列不等式求解即可得出答案;
(3)设利润为15800元,列方程求出![]() ,分三种情况进行讨论,即可解答.
,分三种情况进行讨论,即可解答.
解:(1)设![]() 、
、![]() 两种型号的空调的销售价分别为
两种型号的空调的销售价分别为![]() 、
、![]() 元,
元,
则:![]() 解得:
解得:![]() ,
,
答:![]() 、
、![]() 两种型号空调的销售价分别为2600元和2200元.
两种型号空调的销售价分别为2600元和2200元.
(2)设采购![]() 种型号空调
种型号空调![]() 台,则采购
台,则采购![]() 种型号的空调
种型号的空调![]() 台
台
则![]() ,
,
解得:![]() ,答:最多采购
,答:最多采购![]() 种型号的空调10台.
种型号的空调10台.
(3)根据题意得:
![]() ,解得
,解得![]() ,
,
∵![]() ,∴
,∴![]()
∴共有3种方案:
方案①:![]() 型号空调8台,
型号空调8台,![]() 型号的空调22台;
型号的空调22台;
方案②:![]() 型号空调9台,
型号空调9台,![]() 型号的空调21台;
型号的空调21台;
方案③:![]() 型号空调10台,
型号空调10台,![]() 型号的空调20台.
型号的空调20台.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】已知,关于x的一元二次方程x2+(1﹣k)x﹣k=0 (其中k为常数).
(1)判断方程根的情况并说明理由;
(2)若﹣1<k<0,设方程的两根分别为m,n(m<n),求它的两个根m和n;
(3)在(2)的条件下,若直线y=kx﹣1与x轴交于点C,x轴上另两点A(m,0)、点B(n,0),试说明是否存在k的值,使这三点中相邻两点之间的距离相等?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县某公司参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐助给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量![]() (单位:个)与销售单价
(单位:个)与销售单价![]() (单位:元/个)之间的关系式为
(单位:元/个)之间的关系式为![]() .
.
(1) 若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润![]() (单位:元)与销售单价
(单位:元)与销售单价![]() (单位:元/个)之间的函数关系式;
(单位:元/个)之间的函数关系式;
(2) 在(1)问的条件下,若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人约好步行沿同一路线同一方向在某景点集合,已知甲乙二人相距660米,二人同时出发,走了24分钟时,由于乙距离景点近,先到达等候甲,甲共走了30分钟也到达了景点与乙相遇.在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程![]() (米)与甲出发的时间
(米)与甲出发的时间![]() (分钟)之间的关系如图所示,下列说法错误的是( )
(分钟)之间的关系如图所示,下列说法错误的是( )

A.甲的速度是70米/分B.乙的速度是60米/分
C.甲距离景点2100米D.乙距离景点420米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(p,0),B(0,q),且p、q满足(p﹣2)2+![]() =0.
=0.
(1)求直线AB的解析式;
(2)若点M为直线y=mx上一点,且△ABM是以AB为底的等腰直角三角形,求m值.
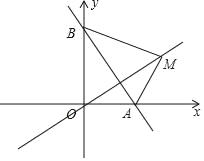
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一辆摩拜单车放在水平的地面上,车把头下方A处与坐垫下方B处在平行于地面的水平线上,A、B之间的距离约为49cm,现测得AC、BC与AB的夹角分别为45°与68°,若点C到地面的距离CD为28cm,坐垫中轴E处与点B的距离BE为4cm,求点E到地面的距离(结果保留一位小数).(参考数据:sin68°≈0.93,cos68°≈0.37,cot68°≈0.40)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应绿色出行号召,越来越多市民选择租用共享单车出行,已知某共享单车公司为市民提供了手机支付和会员卡支付两种支付方式,如图描述了两种方式应支付金额y(元)与骑行时间x(时)之间的函数关系,根据图象回答下列问题:
(1)求手机支付金额y(元)与骑行时间x(时)的函数关系式;
(2)李老师经常骑行共享单车,请根据不同的骑行时间帮他确定选择哪种支付方式比较合算.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:二元一次方程![]() 有无数组解,每组解记为
有无数组解,每组解记为![]() ,称
,称![]() 为亮点,将这些亮点连接得到一条直线,称这条直线是亮点的隐线,答下列问题:
为亮点,将这些亮点连接得到一条直线,称这条直线是亮点的隐线,答下列问题:
(1) 已知![]() ,则是隐线
,则是隐线![]() 的亮点的是 ;
的亮点的是 ;
(2) 设![]() 是隐线
是隐线![]() 的两个亮点,求方程
的两个亮点,求方程![]() 中
中![]() 的最小的正整数解;
的最小的正整数解;
(3)已知![]() 是实数, 且
是实数, 且![]() ,若
,若![]() 是隐线
是隐线![]() 的一个亮点,求隐线
的一个亮点,求隐线![]() 中的最大值和最小值的和.
中的最大值和最小值的和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com