【题目】我县某公司参加社会公益活动，准备购进一批许愿瓶进行销售，并将所得利润捐助给慈善机构．根据市场调查，这种许愿瓶一段时间内的销售量
（单位：个）与销售单价
（单位：元/个）之间的关系式为
．
（1） 若许愿瓶的进价为6元/个，按照上述市场调查的销售规律，求销售利润
（单位：元）与销售单价
（单位：元/个）之间的函数关系式；
（2） 在（1）问的条件下，若许愿瓶的进货成本不超过900元，要想获得最大利润，试确定这种许愿瓶的销售单价，并求出此时的最大利润．
【答案】（1）
；（2）销售单价定为每个15元时，利润最大为1350元．
【解析】试题分析：（1）利用w=销量×每个利润，进而得出函数关系式；
（2）利用进货成本不超过900元，得出x的取值范围，进而得出函数最值．
试题解析：解：（1）由题意得：w=（x﹣6）（﹣30x+600）=﹣30x2+780x﹣3600，∴w与x的函数关系式为w=﹣30x2+780x﹣3600；
（2）由题意得：6（﹣30x+600）≤900，解得：x≥15，在w=﹣30x2+780x﹣3600中，对称轴为：x=﹣
=13．∵a=﹣30，∴当x＞13时，w随x的增大而减小，∴x=15时，w最大为：（15﹣6）（﹣30×15+600）=1350，∴销售单价定为每个15元时，利润最大为1350元．
科目：初中数学 来源： 题型：
【题目】已知直线l1：y＝x+n﹣2与直线l2：y＝mx+n相交于点P（1，2）．
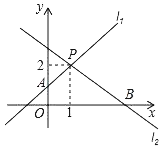
（1）求m，n的值；
（2）请结合图象直接写出不等式mx+n＞x+n﹣2的解集．
（3）若直线l1与y轴交于点A，直线l2与x轴交于点B，求四边形PAOB的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】请阅读下列材料：
问题：如图1，在等边三角形ABC内有一点P，且PA=2，PB=
，PC=1、求∠BPC度数的大小和等边三角形ABC的边长．
李明同学的思路是：将△BPC绕点B逆时针旋转60°，画出旋转后的图形（如图2），连接PP′，可得△P′PC是等边三角形，而△PP′A又是直角三角形（由勾股定理的逆定理可证），从而得到∠BPC=∠AP′B=__________；，进而求出等边△ABC的边长为__________；
问题得到解决．
请你参考李明同学的思路，探究并解决下列问题：如图3，在正方形ABCD内有一点P，且PA=
，BP=
，PC=1．求∠BPC度数的大小和正方形ABCD的边长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】当﹣2＜x＜2时，下列函数中，函数值y随自变量x增大而增大的有（ ）个．
①y=2x；②y=2﹣x；③y=﹣
；④y=x2+6x+8．
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，
在平面直角坐标系
中.
（1）请直接写出点
、
两点的坐标：：___________；：___________；
（2）若把向上平移3个单位，再向右平移2个单位得
，请在上图中画出，并写出点
的坐标___________；
（3）求的面积是多少.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】随着气温的升高，空调的需求量大增.某家电超市对每台进价分别为2000元、1700元的
、
两种型号的空调，近两周的销售情况统计如下：
销售时段 | 销售量 | 销售收入 | |
|
| ||
第一周 | 6台 | 7台 | 31000元 |
第二周 | 8台 | 11台 | 45000元 |
（1）求、两种型号的空调的销售价；
（2）若该家电超市准备用不多于54000元的资金，采购这两种型号的空调30台，求种型号的空调最多能采购多少台？
（3）在（2）的条件下，该家电超市售完这30台空调能否实现利润不低于15800元的目标？若能，请给出采购方案.若不能，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明在课外学习时遇到这样一个问题：
定义：如果二次函数y=a1x2+b1x+c1（a1≠0，a1，b1，c1是常数）与y=a2x2+b2x+c2（a2≠0，a2，b2，c2是常数）满足a1+a2=0，b1=b2，c1+c2=0，则称这两个函数互为“旋转函数”．
求函数y=﹣x2+4x﹣3的“旋转函数”．小明是这样思考的：由函数y=﹣x2+4x﹣3可知，a1=﹣1，b1=4，c1=﹣3，根据a1+a2=0，b1=b2，c1+c2=0，求出a2，b2，c2，就能确定这个函数的“旋转函数”．
（1）请参考小明的方法写出函数y=﹣x2+4x﹣3的“旋转函数”；
（2）若函数
与y=x2﹣3nx+n互为“旋转函数”，求
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某地计划用120～180天（含120与180天）的时间建设一项水利工程，工程需要运送的土石方总量为360万米3．
（1）写出运输公司完成任务所需的时间y（单位：天）与平均每天的工作量x（单位：万米3）之间的函数关系式．并给出自变量x的取值范围；
（2）由于工程进度的需要，实际平均每天运送土石方比原计划多20%，工期比原计划减少了24天，原计划和实际平均每天运送土石方各是多少万米3？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com