
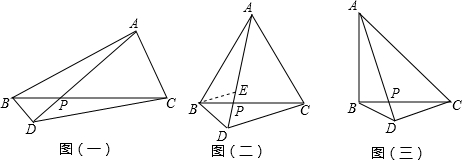
分析 (1)利用全等三角形的性质得到AE=CD,BE=BD,再利用等边三角形的性质得到BD=DE,即可;
(2)利用全等三角形的性质得到AE=CD,BE=BD,再利用勾股定理求出;
(3)判断出△ABE≌△CBD,求出ED=kBD,再利用等腰三角形的三线合一的性质构造出直角三角形,利用三角函数即可;
(4)根据(3)的解决方法,发现规律,从而得到k=sin$\frac{1}{2}α$.
解答 探究:
(1)解:∵△ABE≌△CBD,
∴AE=CD,BE=BD,
∵∠EBD=60°,
∴BD=DE,
∵AD=AE+DE,AD=kDB+DC,
∴AE+DE=kDB+DC,
∴CD+DB=kDB+CD,
∴k=1,
故答案为1.
(2)
作∠DBE=90°,
和(1)方法一样,得出△ABE≌△CBD,
∴BE=BD,AE=CD,
∵AD=AE+ED=CD+ED=kDB+CD,
∴kDB=ED,
在Rt△DBE中,根据勾股定理得,BD2+BE2=DE2
∴BD2+BD2=(kBD)2
∴k=$\sqrt{2}$或k=-$\sqrt{2}$(舍去),
∴AD=kDB+DC等式中k=$\sqrt{2}$.
问题解决:
(3) ①作BF⊥AD,和(1)方法一样,得出△ABE≌△CBD,
①作BF⊥AD,和(1)方法一样,得出△ABE≌△CBD,
∴BE=BD,AE=CD,
∴∠DBF=$\frac{1}{2}$∠DBE=60°,EF=DF,
∵AD=AE+ED,AD=kBD+CD,
∴ED=kBD,
∴DF=$\frac{1}{2}$ED=$\frac{1}{2}$kBD,
在Rt△BFD中,sin∠DFB=$\frac{DF}{BD}$=$\frac{\frac{1}{2}kBD}{BD}$=$\frac{1}{2}$k=$\frac{\sqrt{3}}{2}$,
∴k=$\sqrt{3}$,
∴(k+1)(k-1)=($\sqrt{3}$+1)($\sqrt{3}$-1)=2,
故答案为2.
②解:同(3)①方法一样,得到sin$\frac{1}{2}$α=sin18°=$\frac{1}{2}$k,
∵sin18°=$\frac{\sqrt{5}-1}{4}$
∴k=2×$\frac{\sqrt{5}-1}{4}$=$\frac{\sqrt{5}-1}{2}$,
∴k(k+1)=$\frac{\sqrt{5}-1}{2}$×($\frac{\sqrt{5}-1}{2}$+1)=1
故答案为1.
(4)作BF⊥AD,
和(1)方法一样,得出△ABE≌△CBD,
∴BE=BD,AE=CD,
∴∠DBF=$\frac{1}{2}$∠DBE=$\frac{1}{2}$α,EF=DF,
∵AD=AE+ED,AD=kBD+CD
∴ED=kBD,
∴DF=$\frac{1}{2}$ED=$\frac{1}{2}$kBD,
在Rt△BFD中,sin∠DFB=$\frac{DF}{BD}$=$\frac{\frac{1}{2}kBD}{BD}$=$\frac{1}{2}$k=sin$\frac{1}{2}$α,
∴k=2sin$\frac{1}{2}$α,
故答案为2sin$\frac{1}{2}α$.
点评 本题是相似形的综合题,涉及到的知识点有,全等三角形的判定和性质,由△ABE≌△CBD得出BE=BD,AE=CD,勾股定理BD2+BE2=DE2,锐角的三角函数sin∠DFB=$\frac{DF}{BD}$,解决本题的关键是辅助线的作法.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:选择题
| A. | 一、二 | B. | 三、四 | C. | 一、二、三 | D. | 一、三、四 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直线y=kx+b交坐标轴于A(-5,0),B(0,7)两点,则不等式kx+b>0的解集是( )
如图,直线y=kx+b交坐标轴于A(-5,0),B(0,7)两点,则不等式kx+b>0的解集是( )| A. | x<-5 | B. | x>-5 | C. | x>7 | D. | x<-7 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x(10÷2+x)=6 | B. | x(10÷2-x)=6 | C. | x(10-x)=6 | D. | x(x-1)=28 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com