
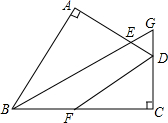
 如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,BE、CD交于G点
如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,BE、CD交于G点分析 (1)根据多边形的内角和定理求出即可;
(2)根据角平分线定义求出∠CDF+∠GBC=90°,根据三角形内角和定理求出∠CDF+∠DFC=90°,推出∠DFC=∠GBC,根据平行线的判定得出BG∥DF,根据平行线的性质得出即可.
解答 证明:(1)∵四边形ABCD中,∠A=∠C=90°,∠A+∠ABC+∠C+∠ADC=360°,
∴∠ABC+∠ADC=180°;
(2)∵BE平分∠ABC,DF平分∠ADC,
∴∠GBC=$\frac{1}{2}$∠ABC,∠CDF=$\frac{1}{2}$∠ADC,
∵∠ABC+∠ADC=180°,
∴∠GBC+∠CDF=90°,
∵∠C+∠CDF+∠DFC=180°,∠C=90°,
∴∠CDF+∠DFC=90°,
∴∠GBC=∠DFC,
∴BG∥DF,
∴∠G=∠CDF.
点评 本题考查了平行线的性质和判定,三角形的内角和定理,角平分线定义的应用,能求出BG∥DF是解此题的关键,注意:两直线平行,同位角相等.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
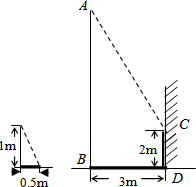 如图,某一时刻,小明垂直地面竖起一根1m高的直杆,量得其在阳光下的影长为0.5m,此时,旁边一电线杆AB在阳光下的影子分别落在了地上和墙上,他又量得电线杆AB落在地面上的影子部分BD长为3m,落在墙上的影子部分CD高为2m,小明用这些数据很快算出了电线杆AB的高,请你计算一下:
如图,某一时刻,小明垂直地面竖起一根1m高的直杆,量得其在阳光下的影长为0.5m,此时,旁边一电线杆AB在阳光下的影子分别落在了地上和墙上,他又量得电线杆AB落在地面上的影子部分BD长为3m,落在墙上的影子部分CD高为2m,小明用这些数据很快算出了电线杆AB的高,请你计算一下:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
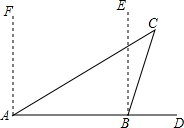 如图,一艘轮船上午8时在A处沿正东方向行驶,在A处测得灯塔C在北偏东60°方向上,行驶1小时后到达B处,在B处测得灯塔C在北偏东20°方向上.求△ABC各内角及∠DBC的度数.
如图,一艘轮船上午8时在A处沿正东方向行驶,在A处测得灯塔C在北偏东60°方向上,行驶1小时后到达B处,在B处测得灯塔C在北偏东20°方向上.求△ABC各内角及∠DBC的度数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com