
【题目】(探究发现)
如图1,在△ABC中,点P是内角∠ABC和外角∠ACD的角平分线的交点,试猜想∠P与∠A之间的数量关系,并证明你的猜想.

(迁移拓展)
如图2,在△ABC中,点P是内角∠ABC和外角∠ACD的n等分线的交点,即∠PBC=![]() ∠ABC,∠PCD=
∠ABC,∠PCD=![]() ∠ACD,
∠ACD,
试猜想∠P与∠A之间的数量关系,并证明你的猜想.
(应用创新)
已知,如图3,AD、BE相交于点C,∠ABC、∠CDE、∠ACE的角平分线交于点P,∠A=35°,∠E=25°,则∠BPD= .
【答案】(1)∠A=2∠P;(2)∠A=n∠P;(3)30°.
【解析】
(1)根据角平分线的定义以及一个三角形的外角等于与它不相邻的两个内角和,可求出∠A的度数,根据补角的定义求出∠ACB的度数,根据三角形的内角和即可求出∠P的度数,即可求出结果;
(2)根据已知条件以及一个三角形的外角等于与它不相邻的两个内角和,可求出∠A的度数,根据补角的定义求出∠ACB的度数,根据三角形的内角和即可求出∠P的度数,即可求出结果;
(3)根据(1)的结论即可得到结果.
解:(1)∠A=2∠P,理由如下:
∵BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,
∴∠PBC=![]() ∠ABC,∠PCD=
∠ABC,∠PCD=![]() ∠ACD,
∠ACD,
∵∠ACD是△ABC的外角,∠PCD是△BPC的外角,
∴∠ACD=∠ABC+∠A,∠PCD=∠PBC+∠P,
∴![]() ∠ACD=
∠ACD=![]() ∠ABC+
∠ABC+![]() ∠A,
∠A,
∴![]() ∠ABC+
∠ABC+![]() ∠A=∠PBC+∠P,
∠A=∠PBC+∠P,
∴∠A=2∠P;
(2)∠A=n∠P,理由如下:
∵点P是内角∠ABC和外角∠ACD的n等分线的交点,
∴∠PBC=![]() ∠ABC,∠PCD=
∠ABC,∠PCD=![]() ∠ACE.
∠ACE.
∵∠ACD是△ABC的外角,∠PCD是△BPC的外角,
∴∠ACD=∠ABC+∠A,∠PCD=∠PBC+∠P,
∴![]() ∠ACD=
∠ACD=![]() ∠ABC+
∠ABC+![]() ∠A,
∠A,
∴![]() ∠ABC+
∠ABC+![]() ∠A=∠PBC+∠P,
∠A=∠PBC+∠P,
∴∠A=n∠P;
(3)∵∠ABC、∠CDE、∠ACE的角平分线交于点P,
∴由(1)的结论知,∠BPC=![]() ∠A=
∠A=![]() °,∠CPD=
°,∠CPD=![]() ∠E=
∠E=![]() °,
°,
∴∠BPD=∠BPC+∠DPC=30°,
故答案为:30°.


科目:初中数学 来源: 题型:
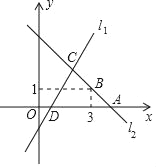
【题目】如图,直线l1的解析式为y=2x﹣2,直线l1与x轴交于点D,直线l2:y=kx+b与x轴交于点A,且经过点B,直线l1、l2交于点C(m,2).
(1)求m;
(2)求直线l2的解析式;
(3)根据图象,直接写出1<kx+b<2x﹣2的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,回答有关问题:在实数这章中,遇到过![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 这样的式子,我们把这样的式子叫做二次根式,根号下的数叫做被开方数.如果一个二次根式的被开方数中有的因数能开得尽方,可以利用
这样的式子,我们把这样的式子叫做二次根式,根号下的数叫做被开方数.如果一个二次根式的被开方数中有的因数能开得尽方,可以利用![]() =
=![]() (a≥0,b≥0);
(a≥0,b≥0);![]() (a≥0,b>0)将这些因数开出来,从而将二次根式化简.当一个二次根式的被开方数中不含开得尽方的因数或者被开方数中不含有分母时,这样的二次根式叫做最简二次根式,例如,
(a≥0,b>0)将这些因数开出来,从而将二次根式化简.当一个二次根式的被开方数中不含开得尽方的因数或者被开方数中不含有分母时,这样的二次根式叫做最简二次根式,例如,![]() 化成最简二次根式是
化成最简二次根式是![]() ,
,![]() 化成最简二次根式是3
化成最简二次根式是3![]() ,几个二次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式叫做同类二次根式,如上面的例子中的
,几个二次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式叫做同类二次根式,如上面的例子中的![]() 和
和![]() 就是同类二次根式.
就是同类二次根式.
(1)请判断下列各式中,哪些是同类二次根式?![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)二次根式中的同类二次根式可以像整式中的同类项一样合并,请计算:![]() +
+![]() -
-![]() -
-![]() +
+![]() -
-![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人以各自的交通工具、相同路线,前往距离单位10km的培训中心参加学习.图中l甲、l乙分别表示甲、乙前往目的地所走的路程S(km)随时间t(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②乙走了8km后遇到甲;③乙出发6分钟后追上甲;④甲走了28分钟时,甲乙相距3km.其中正确的是( )

A. 只有① B. ①③ C. ②③④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
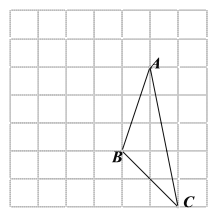
【题目】画图(只能借助于网格)并填空:
如图,每个小正方形的边长为![]() 个单位,每个小正方形的顶点叫格点.
个单位,每个小正方形的顶点叫格点.
(1)将![]() 向左平移
向左平移![]() 格,再向上平移
格,再向上平移![]() 格,请在图中画出平移后的
格,请在图中画出平移后的![]() ;
;
(2)![]() 的面积为 ;
的面积为 ;
(3)利用网格在图中画出△ABC的中线![]() ,高线
,高线![]() ;
;
(4)在图中能使![]() 的格点
的格点![]() 的个数有 个(点
的个数有 个(点![]() 异于
异于![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=60°,AB=2,E是DC边上一个动点,F是AB边上一点,∠AEF=30°.设DE=x,图中某条线段长为y,y与x满足的函数关系的图象大致如图所示,则这条线段可能是图中的( ).

A. 线段EC B. 线段AE C. 线段EF D. 线段BF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,一次函数的图象经过点A(2,3)与点B(0,5).
(1)求此一次函数的表达式;
(2)若点P为此一次函数图象上一点,且△POB的面积为10,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(a,b),B(c,0),|a-3|+(2b-c)2+![]() =0.
=0.

(1)求点A,B的坐标;
(2)如图,点C为x轴正半轴上一点,且OC=OA,点D为OC的中点,连AC,AD,请探索AD+CD与![]() AC之间的大小关系,并说明理由;
AC之间的大小关系,并说明理由;

(3)如图,过点A作AE⊥y轴于E,F为x轴负半轴上一动点( 不与(-3,0)重合 ),G在EF延长线上,以EG为一边作∠GEN=45°,过A作AM⊥x轴,交EN于点M,连FM,当点F在x轴负半轴上移动时,式子![]() 的值是否发生变化?若变化,求出变化的范围;若不变化,请求出其值并说明理由.
的值是否发生变化?若变化,求出变化的范围;若不变化,请求出其值并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象l与坐标轴分别交于点E,F,与双曲线y=﹣ ![]() (x<0)交于点P(﹣1,n),且F是PE的中点,直线x=a与l交于点A,与双曲线交于点B(不同于A),PA=PB,则a= .
(x<0)交于点P(﹣1,n),且F是PE的中点,直线x=a与l交于点A,与双曲线交于点B(不同于A),PA=PB,则a= . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com