
【题目】如图,一次函数y=kx+b的图象l与坐标轴分别交于点E,F,与双曲线y=﹣ ![]() (x<0)交于点P(﹣1,n),且F是PE的中点,直线x=a与l交于点A,与双曲线交于点B(不同于A),PA=PB,则a= .
(x<0)交于点P(﹣1,n),且F是PE的中点,直线x=a与l交于点A,与双曲线交于点B(不同于A),PA=PB,则a= . 
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:
【题目】(探究发现)
如图1,在△ABC中,点P是内角∠ABC和外角∠ACD的角平分线的交点,试猜想∠P与∠A之间的数量关系,并证明你的猜想.

(迁移拓展)
如图2,在△ABC中,点P是内角∠ABC和外角∠ACD的n等分线的交点,即∠PBC=![]() ∠ABC,∠PCD=
∠ABC,∠PCD=![]() ∠ACD,
∠ACD,
试猜想∠P与∠A之间的数量关系,并证明你的猜想.
(应用创新)
已知,如图3,AD、BE相交于点C,∠ABC、∠CDE、∠ACE的角平分线交于点P,∠A=35°,∠E=25°,则∠BPD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架长25米的梯子,斜靠在竖直的墙上,这时梯子底端离墙7米.
(1)此时梯子顶端离地面多少米?
(2)若梯子顶端下滑4米,那么梯子底端将向左滑动多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C.
(1)求抛物线的函数解析式.
(2)设点D在抛物线上,点E在抛物线的对称轴上,若四边形AODE是平行四边形,求点D的坐标.
(3)联接BC交x轴于点F.y轴上是否存在点P,使得△POC与△BOF相似?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,AE平分∠BAD,交BC于E,DE⊥AE,下列结论::①DE平分∠ADC;②E是BC的中点;③AD=2CD;④梯形ADCE的面积与△ABE的面积比是3:1,其中正确的结论的个数有( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AE平分∠BAD,交BC于E,过E做EF⊥AD于F,连接BF交AE于P,连接PD.
(1)求证:四边形ABEF是正方形;
(2)如果AB=6,AD=8,求tan∠ADP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下是两张不同类型火车的车票(“![]() 次”表示动车,“
次”表示动车,“![]() 次”表示高铁):
次”表示高铁):

⑴根据车票中的信息填空:该列动车和高铁是__ _向而行(填“相”或“同”).
⑵知该列动车和高铁的平均速度分别为![]() 、
、![]() ,两列火车的长度不计.
,两列火车的长度不计.
通过测算,如果两列火车直达终点(即中途都不停靠任何站点),高铁比动车将早到![]() ,求
,求![]() 、
、![]() 两地之间的距离.
两地之间的距离.
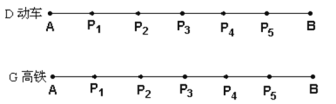
②在①中测算的数据基础上,已知![]() 、
、![]() 两地途中依次设有
两地途中依次设有![]() 个站点
个站点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,且
,且![]() ,动车每个站点都停靠,高铁只停靠
,动车每个站点都停靠,高铁只停靠![]() 、
、![]() 两个站点,两列火车在每个停靠站点都停留
两个站点,两列火车在每个停靠站点都停留![]() .求该列高铁追上动车的时刻.
.求该列高铁追上动车的时刻.
查看答案和解析>>
科目:初中数学 来源: 题型:
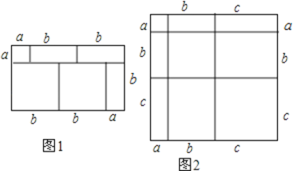
【题目】我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.例如图可以得到(a+2b)(a+b)=a2+3ab+2b2.请解答下列问题:
(1)写出图2所表示的数学等式;
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)小明同学用3张边长为a的正方形,4张边长为b的正方形,7张边长分别为a、b的长方形纸片拼出了一个长方形,那么该长方形较长一边的边长为多少?
(4)小明同学又用x张边长为a的正方形,y张边长为b的正方形,z张边长分别为a、b的长方形纸片拼出了一个面积为(5a+7b)(4a+9b)长方形,那么x+y+z= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,E、F均为中点,则下列结论中:①AF⊥DE;②AD=BP;③PE+PF= ![]() PC;④PE+PF=PC.其中正确的是 .
PC;④PE+PF=PC.其中正确的是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com