
分析 (1)设乙盒中蓝球的个数为x,根据“乙盒中任意摸取一球为蓝球的概率是从甲盒中任意摸取一球为蓝球的概率的2倍”列方程求解可得;
(2)画树状图列出所有等可能结果,根据概率公式求解可得.
解答 解:(1)设乙盒中蓝球的个数为x,
根据题意,得:$\frac{x}{x+1}$=2×$\frac{1}{3}$,
解得:x=2,
答:乙盒中蓝球的个数为2;
(2)画树状图如下: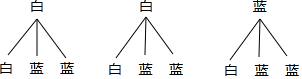
由于共有9种等可能情况,其中两球均为蓝球的有2种,
∴这两球均为蓝球的概率为$\frac{2}{9}$.
点评 本题考查的是用列表法或画树状图法求概率与古典概率的知识.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D的切线交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D的切线交BC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①③ | B. | ①② | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于C,D两点,与x,y轴交于B,A两点,且tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.
如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于C,D两点,与x,y轴交于B,A两点,且tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com