
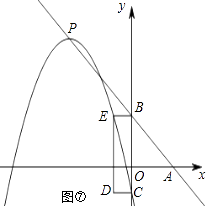
【题目】如图,在平面直角坐标系中,直线y=﹣x+4与x轴、y轴分别交于点A、B.抛物线y=﹣ ![]() +n的顶点P在直线y=﹣x+4上,与y轴交于点C(点P、C不与点B重合),以BC为边作矩形BCDE,且CD=2,点P、D在y轴的同侧.
+n的顶点P在直线y=﹣x+4上,与y轴交于点C(点P、C不与点B重合),以BC为边作矩形BCDE,且CD=2,点P、D在y轴的同侧.
(1)n=(用含m的代数式表示),点C的纵坐标是(用含m的代数式表示).
(2)当点P在矩形BCDE的边DE上,且在第一象限时,求抛物线对应的函数表达式.
(3)设矩形BCDE的周长为d(d>0),求d与m之间的函数表达式.
(4)直接写出矩形BCDE有两个顶点落在抛物线上时m的值.
【答案】
(1)﹣m+4;﹣ ![]() m2﹣m+4
m2﹣m+4
(2)
解:∵四边形BCDE是矩形,
∴DE∥y轴.
∵CD=2,
∴当x=2时,y=2.
∴DE与AB的交点坐标为(2,2).
∴当点P在矩形BCDE的边DE上时,抛物线的顶点P坐标为(2,2).
∴抛物线对应的函数表达式为 ![]()
(3)
解:∵直线y=﹣x+4与y轴交于点B,
∴点B的坐标是(0,4).
当点B与点C重合时, ![]() .
.
解得m1=0,m2=﹣3.
i)当m<﹣3或m>0时,如图①、②, ![]() .
. ![]() .
.
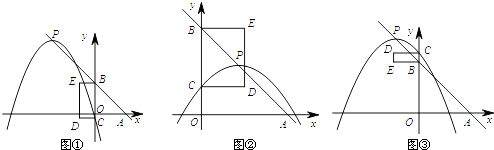
ii)当﹣3<m<0时,如图③, ![]() .
. ![]()
(4)
解:如图④⑤,点C、D在抛物线上时,由CD=2可知对称轴为:x=±1,即m=±1;
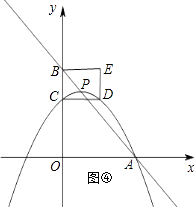
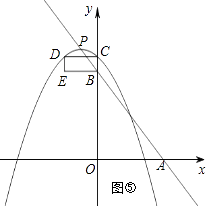
如图⑥⑦,点C、E在抛物线上时,由B(0,4)和CD=2得:E(﹣2,4)
则4=﹣ ![]() (﹣2﹣m)2+(﹣m+4),解得:
(﹣2﹣m)2+(﹣m+4),解得: ![]() 、
、 ![]() .
.
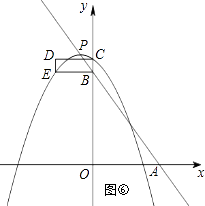
综上所述:m=1、m=﹣1、 ![]() 、
、 ![]() .
.
【解析】解:(1)y=﹣ ![]() (x﹣m)2+n=﹣
(x﹣m)2+n=﹣ ![]() x2+
x2+ ![]() mx﹣
mx﹣ ![]() m2+n,
m2+n,
∴P(m,n),
∵点P在直线y=﹣x+4上,
∴n=﹣m+4,
当x=0时,y=﹣ ![]() m2+n=﹣
m2+n=﹣ ![]() m2﹣m+4,
m2﹣m+4,
即点C的纵坐标为:﹣ ![]() m2﹣m+4,
m2﹣m+4,
所以答案是:﹣m+4,﹣ ![]() m2﹣m+4;
m2﹣m+4;


 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】已知正方形ABCD,点M边AB的中点.
(1)如图1,点G为线段CM上的一点,且∠AGB=90°,延长AG、BG分别与边BC、CD交于点E、F.
①求证:BE=CF;
②求证:BE2=BCCE.
(2)如图2,在边BC上取一点E,满足BE2=BCCE,连接AE交CM于点G,连接BG并延长CD于点F,求tan∠CBF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行八百米跑体能测试,测试结果分为A、B、C、D四个等级,请根据两幅统计图中的信息回答下列问题: 
(1)求本次测试共调查了多少名学生?
(2)求本次测试结果为B等级的学生数,并补全条形统计图;
(3)若该中学八年级共有900名学生,请你估计八年级学生中体能测试结果为D等级的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向C处,测得∠CAO=45°,轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45km/h和36km/h,经过0.1h,轮船甲行驶至B处,轮船乙行驶至D处,测得∠DBO=58°,此时B处距离码头O多远?(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把大小完全相同的6个乒乓球分成两组,每组3个,每组乒乓球上面分别标有数字1,2,3,将这两组乒乓球分别放入两个盒子中搅匀,再从每个盒子中各随机取出1个乒乓球,请用画树状图(或列表)的方法,求取出的2个乒乓球上面数字之和为偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.给出以下结论:①DG=DF;②四边形EFDG是菱形;③EG2= ![]() GF×AF;④当AG=6,EG=2
GF×AF;④当AG=6,EG=2 ![]() 时,BE的长为
时,BE的长为 ![]()
![]() ,其中正确的结论个数是( )
,其中正确的结论个数是( ) 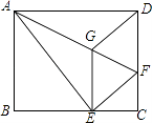
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的面积为16,点D是BC边上一点,且BD= ![]() BC,点G是AB上一点,点B在△ABC内部,且四边形BDHG是平行四边形,则图中阴影部分的面积是 .
BC,点G是AB上一点,点B在△ABC内部,且四边形BDHG是平行四边形,则图中阴影部分的面积是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com