
【题目】已知正方形ABCD,点M边AB的中点.
(1)如图1,点G为线段CM上的一点,且∠AGB=90°,延长AG、BG分别与边BC、CD交于点E、F.
①求证:BE=CF;
②求证:BE2=BCCE.
(2)如图2,在边BC上取一点E,满足BE2=BCCE,连接AE交CM于点G,连接BG并延长CD于点F,求tan∠CBF的值.
【答案】
(1)
解:①∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠BCF=90°,
∴∠ABG+∠CBF=90°,
∵∠AGB=90°,
∴∠ABG+∠BAG=90°,
∴∠BAG=∠CBF,
∵AB=BC,∠ABE=∠BCF=90°,
∴△ABE≌△BCF,
∴BE=CF,
②∵∠AGB=90°,点M为AB的中点,
∴MG=MA=MB,
∴∠GAM=∠AGM,
又∵∠CGE=∠AGM,∠GAM=∠CBG,
∴∠CGE=∠CBG,
又∠ECG=∠GCB,
∴△CGE∽△CBG,
∴ ![]() =
= ![]() ,即CG2=BCCE,
,即CG2=BCCE,
由∠CFG=∠GBM=∠BGM=∠CGF得CF=CG,
由①知BE=CF,
∴BE=CG,
∴BE2=BCCE;
(2)
解:延长AE、DC交于点N,
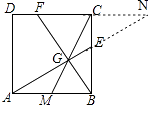
∵四边形ABCD是正方形,
∴AB∥CD,
∴∠N=∠EAB,
又∵∠CEN=∠BEA,
∴△CEN∽△BEA,
∴ ![]() =
= ![]() ,即BECN=ABCE,
,即BECN=ABCE,
∵AB=BC,BE2=BCCE,
∴CN=BE,
∵AB∥DN,
∴ ![]() =
= ![]() =
= ![]() ,
,
∵AM=MB,
∴FC=CN=BE,
不妨设正方形的边长为1,BE=x,
由BE2=BCCE可得x2=1(1﹣x),
解得:x1= ![]() ,x2=
,x2= ![]() (舍),
(舍),
∴ ![]() =
= ![]() ,
,
则tan∠CBF= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)①由正方形的性质知AB=BC、∠ABC=∠BCF=90°、∠ABG+∠CBF=90°,结合∠ABG+∠BAG=90°可得∠BAG=∠CBF,证△ABE≌△BCF可得;
②由RtABG斜边AB中线知MG=MA=MB,即∠GAM=∠AGM,结合∠CGE=∠AGM、∠GAM=∠CBG知∠CGE=∠CBG,从而证△CGE∽△CBG得CG2=BCCE,由BE=CF=CG可得答案;(2)延长AE、DC交于点N,证△CEN∽△BEA得BECN=ABCE,由AB=BC、BE2=BCCE知CN=BE,再由 ![]() =
= ![]() =
= ![]() 且AM=MB得FC=CN=BE,设正方形的边长为1、BE=x,根据BE2=BCCE求得BE的长,最后由tan∠CBF=
且AM=MB得FC=CN=BE,设正方形的边长为1、BE=x,根据BE2=BCCE求得BE的长,最后由tan∠CBF= ![]() =
= ![]() 可得答案.
可得答案.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方,以及对相似三角形的应用的理解,了解测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】如图1,⊙O的直径AB=12,P是弦BC上一动点(与点B,C不重合),∠ABC=30°,过点P作PD⊥OP交⊙O于点D. 
(1)如图2,当PD∥AB时,求PD的长;
(2)如图3,当 ![]() =
= ![]() 时,延长AB至点E,使BE=
时,延长AB至点E,使BE= ![]() AB,连接DE. ①求证:DE是⊙O的切线;
AB,连接DE. ①求证:DE是⊙O的切线;
②求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c与反比例函数y= ![]() 的图象在第一象限有一个公共点,其横坐标为1,则一次函数y=bx+ac的图象可能是( )
的图象在第一象限有一个公共点,其横坐标为1,则一次函数y=bx+ac的图象可能是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解
我们知道,1+2+3+…+n= ![]() ,那么12+22+32+…+n2结果等于多少呢?
,那么12+22+32+…+n2结果等于多少呢?
在图1所示三角形数阵中,第1行圆圈中的数为1,即12 , 第2行两个圆圈中数的和为2+2,即22 , …;第n行n个圆圈中数的和为 ![]() ,即n2 , 这样,该三角形数阵中共有
,即n2 , 这样,该三角形数阵中共有 ![]() 个圆圈,所有圆圈中数的和为12+22+32+…+n2 .
个圆圈,所有圆圈中数的和为12+22+32+…+n2 . 
(1)将三角形数阵经两次旋转可得如图2所示的三角形数阵,观察这三个三角形数阵各行同一位置圆圈中的数(如第n﹣1行的第一个圆圈中的数分别为n﹣1,2,n),发现每个位置上三个圆圈中数的和均为 , 由此可得,这三个三角形数阵所有圆圈中数的总和为3(12+22+32+…+n2)= , 因此,12+22+32+…+n2= .
(2)根据以上发现,计算: ![]() 的结果为 .
的结果为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数y= ![]() (x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3,
(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3, 
(1)求反比例函数y= ![]() 的解析式;
的解析式;
(2)求cos∠OAB的值;
(3)求经过C、D两点的一次函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣x+4与x轴、y轴分别交于点A、B.抛物线y=﹣ ![]() +n的顶点P在直线y=﹣x+4上,与y轴交于点C(点P、C不与点B重合),以BC为边作矩形BCDE,且CD=2,点P、D在y轴的同侧.
+n的顶点P在直线y=﹣x+4上,与y轴交于点C(点P、C不与点B重合),以BC为边作矩形BCDE,且CD=2,点P、D在y轴的同侧.
(1)n=(用含m的代数式表示),点C的纵坐标是(用含m的代数式表示).
(2)当点P在矩形BCDE的边DE上,且在第一象限时,求抛物线对应的函数表达式.
(3)设矩形BCDE的周长为d(d>0),求d与m之间的函数表达式.
(4)直接写出矩形BCDE有两个顶点落在抛物线上时m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com