
分析 (1)设购买A型公交车每辆需x万元,购买B型公交车每辆需y万元,根据“A型公交车1辆,B型公交车2辆,共需400万元;A型公交车2辆,B型公交车1辆,共需350万元”列出方程组解决问题;
(2)设购买A型公交车a辆,则B型公交车(10-a)辆,由“购买A型和B型公交车的总费用不超过1220万元”和“10辆公交车在该线路的年均载客总和不少于650万人次”列出不等式组探讨得出答案即可.
解答 解:(1)设购买A型公交车每辆需x万元,购买B型公交车每辆需y万元,由题意得
$\left\{\begin{array}{l}{x+2y=400}\\{2x+y=350}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=100}\\{y=150}\end{array}\right.$,
答:购买A型公交车每辆需100万元,购买B型公交车每辆需150万元.
(2)设购买A型公交车a辆,则B型公交车(10-a)辆,由题意得
$\left\{\begin{array}{l}{100a+150(10-a)≤1220}\\{60a+100(10-a)≥650}\end{array}\right.$,
解得:$\frac{28}{5}$≤a≤$\frac{35}{4}$,
因为a是整数,
所以a=6,7,8;
则(10-a)=4,3,2;
三种方案:
①购买A型公交车6辆,则B型公交车4辆:100×6+150×4=1200万元;
②购买A型公交车7辆,则B型公交车3辆:100×7+150×3=1150万元;
③购买A型公交车8辆,则B型公交车2辆:100×8+150×2=1100万元;
购买A型公交车8辆,则B型公交车2辆费用最少,最少总费用为1100万元.
点评 此题考查二元一次方程组和一元一次不等式组的应用,注意理解题意,找出题目蕴含的数量关系,列出方程组或不等式组解决问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
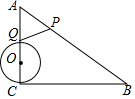 如图,Rt△ACB中,∠C=90°,AC=3,BC=4,半径为1的⊙O,圆心O在AC上且与BC相切,P是线段AB上的动点,过点P作⊙O的一条切线PQ,Q为切点,则PQ的最小值为$\frac{\sqrt{39}}{5}$.
如图,Rt△ACB中,∠C=90°,AC=3,BC=4,半径为1的⊙O,圆心O在AC上且与BC相切,P是线段AB上的动点,过点P作⊙O的一条切线PQ,Q为切点,则PQ的最小值为$\frac{\sqrt{39}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
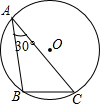 如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则劣弧$\widehat{BC}$的长等于( )
如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则劣弧$\widehat{BC}$的长等于( )| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{2\sqrt{3}π}{3}$ | D. | $\frac{\sqrt{3}π}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 一副三角尺按如图的位置摆放(顶点C 与F 重合,边CA与边FE叠合,顶点B、C、D在一条直线上).将三角尺DEF绕着点F按顺时针方向旋转n°后(0<n<180 ),如果EF∥AB,那么n的值是45.
一副三角尺按如图的位置摆放(顶点C 与F 重合,边CA与边FE叠合,顶点B、C、D在一条直线上).将三角尺DEF绕着点F按顺时针方向旋转n°后(0<n<180 ),如果EF∥AB,那么n的值是45.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
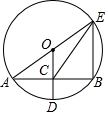 如图,⊙O的半径OD垂直于弦AB,垂足为点C,连接AO并延长交⊙O于点E,连接BE,CE.若AB=8,CD=2,则△BCE的面积为( )
如图,⊙O的半径OD垂直于弦AB,垂足为点C,连接AO并延长交⊙O于点E,连接BE,CE.若AB=8,CD=2,则△BCE的面积为( )| A. | 12 | B. | 15 | C. | 16 | D. | 18 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
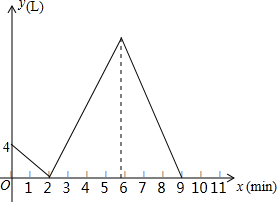 某容器装有一个进水管和一个出水管,从某时刻开始2min内既进水又出水,在随后的4min内只进水不出水,之后关闭进水管,打开出水管,容器内的水量y(L)与时间x(min)之间的函数图象如图所示.
某容器装有一个进水管和一个出水管,从某时刻开始2min内既进水又出水,在随后的4min内只进水不出水,之后关闭进水管,打开出水管,容器内的水量y(L)与时间x(min)之间的函数图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com