
分析 (Ⅰ)把M点坐标代入抛物线解析式可得到b与a的关系,可用a表示出抛物线解析式,化为顶点式可求得其顶点坐标;
(Ⅱ)由直线解析式可先求得m的值,联立直线与抛物线解析式,消去y,可得到关于x的一元二次方程,再判断其判别式大于0即可;
(Ⅲ)(i)由(Ⅱ)的方程,可求得N点坐标,利用勾股定理可求得MN2,利用二次函数性质可求得MN长度的取值范围;(ii)设抛物线对称轴交直线与点E,则可求得E点坐标,利用S△QMN=S△QEN+S△QEM可用a表示出△QMN的面积,再整理成关于a的一元二次方程,利用判别式可得其面积的取值范围,可求得答案.
解答 解:
(Ⅰ)∵抛物线y=ax2+ax+b过点M(1,0),
∴a+a+b=0,即b=-2a,
∴y=ax2+ax+b=ax2+ax-2a=a(x+$\frac{1}{2}$)2-$\frac{9a}{4}$,
∴抛物线顶点Q的坐标为(-$\frac{1}{2}$,-$\frac{9a}{4}$);
(Ⅱ)∵直线y=2x+m经过点M(1,0),
∴0=2×1+m,解得m=-2,
联立直线与抛物线解析式,消去y可得ax2+(a-2)x-2a+2=0(*)
∴△=(a-2)2-4a(-2a+2)=9a2-12a+4,
由(Ⅰ)知b=-2a,且a<b,
∴a<0,b>0,
∴△>0,
∴方程(*)有两个不相等的实数根,
∴直线与抛物线有两个交点;
(Ⅲ)联立直线与抛物线解析式,消去y可得ax2+(a-2)x-2a+2=0,即x2+(1-$\frac{2}{a}$)x-2+$\frac{2}{a}$=0,
∴(x-1)[x-($\frac{2}{a}$-2)]=0,解得x=1或x=$\frac{2}{a}$-2,
∴N点坐标为($\frac{2}{a}$-2,$\frac{4}{a}$-6),
(i)由勾股定理可得MN2=[($\frac{2}{a}$-2)-1]2+($\frac{4}{a}$-6)2=$\frac{20}{{a}^{2}}$-$\frac{60}{a}$+45=20($\frac{1}{a}$-$\frac{3}{2}$)2,
∵-1≤a≤-$\frac{1}{2}$,
∴-2≤$\frac{1}{a}$≤-1,
∴MN2随$\frac{1}{a}$的增大而减小,
∴当$\frac{1}{a}$=-2时,MN2有最大值245,则MN有最大值7$\sqrt{5}$,
当$\frac{1}{a}$=-1时,MN2有最小值125,则MN有最小值5$\sqrt{5}$,
∴线段MN长度的取值范围为5$\sqrt{5}$≤MN≤7$\sqrt{5}$;
(ii)如图,设抛物线对称轴交直线与点E,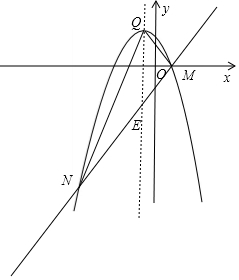
∵抛物线对称轴为x=-$\frac{1}{2}$,
∴E(-$\frac{1}{2}$,-3),
∵M(1,0),N($\frac{2}{a}$-2,$\frac{4}{a}$-6),且a<0,设△QMN的面积为S,
∴S=S△QEN+S△QEM=$\frac{1}{2}$|($\frac{2}{a}$-2)-1|•|-$\frac{9a}{4}$-(-3)|=$\frac{27}{4}$-$\frac{3}{a}$-$\frac{27a}{8}$,
∴27a2+(8S-54)a+24=0(*),
∵关于a的方程(*)有实数根,
∴△=(8S-54)2-4×27×24≥0,即(8S-54)2≥(36$\sqrt{2}$)2,
∵a<0,
∴S=$\frac{27}{4}$-$\frac{3}{a}$-$\frac{27a}{8}$>$\frac{27}{4}$,
∴8S-54>0,
∴8S-54≥36$\sqrt{2}$,即S≥$\frac{27}{4}$+$\frac{9\sqrt{2}}{2}$,
当S=$\frac{27}{4}$+$\frac{9\sqrt{2}}{2}$时,由方程(*)可得a=-$\frac{2\sqrt{2}}{3}$满足题意,
∴当a=-$\frac{2\sqrt{2}}{3}$,b=$\frac{4\sqrt{2}}{3}$时,△QMN面积的最小值为$\frac{27}{4}$+$\frac{9\sqrt{2}}{2}$.
点评 本题为二次函数的综合应用,涉及函数图象的交点、二次函数的性质、根的判别式、勾股定理、三角形的面积等知识.在(1)中由M的坐标得到b与a的关系是解题的关键,在(2)中联立两函数解析式,得到关于x的一元二次方程是解题的关键,在(3)中求得N点的坐标是解题的关键,在最后一小题中用a表示出△QMN的面积是解题的关键.本题考查知识点较多,综合性较强,难度较大.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:选择题
| 女生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 成绩/个 | 48 | 49 | 52 | 47 | 51 | 53 | 52 | 49 | 51 | 49 |
| A. | 52,51 | B. | 51,51 | C. | 49,49 | D. | 49,50 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知,如图,△ABC是等边三角形,四边形BDEF是菱形,其中线段DF的长与DB相等,将菱形BDEF绕点B按顺时针方向旋转,甲、乙两位同学发现在此旋转过程中,有如下结论.
已知,如图,△ABC是等边三角形,四边形BDEF是菱形,其中线段DF的长与DB相等,将菱形BDEF绕点B按顺时针方向旋转,甲、乙两位同学发现在此旋转过程中,有如下结论.| A. | 甲、乙都对 | B. | 乙对甲不对 | C. | 甲对乙不对 | D. | 甲、乙都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
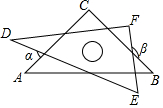 小明把一副含45°,30°的直角三角板如图摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于( )
小明把一副含45°,30°的直角三角板如图摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于( )| A. | 180° | B. | 210° | C. | 360° | D. | 270° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
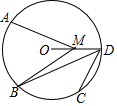 如图,A,B,C,D是⊙O上的四个点,B是$\widehat{AC}$的中点,M是半径OD上任意一点.若∠BDC=40°,则∠AMB的度数不可能是( )
如图,A,B,C,D是⊙O上的四个点,B是$\widehat{AC}$的中点,M是半径OD上任意一点.若∠BDC=40°,则∠AMB的度数不可能是( )| A. | 45° | B. | 60° | C. | 75° | D. | 85° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com