
| 女生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 成绩/个 | 48 | 49 | 52 | 47 | 51 | 53 | 52 | 49 | 51 | 49 |
| A. | 52,51 | B. | 51,51 | C. | 49,49 | D. | 49,50 |
分析 根据众数与中位数的定义,众数是出现次数最多的一个,中位数应是把10个数据按从小到大的顺序排列后第5个和第6个数据的平均数解答即可.
解答 解:把这些数从小到大排列为47,48,49,49,49,51,51,52,52,53,
最中间两个数的平均数是:$\frac{49+51}{2}$=50,
则中位数是50;
数据49出现了3次,出现次数最多,所以这组数据的众数为49.
故选D.
点评 本题考查了中位数和众数:在一组数据中出现次数最多的数据叫做众数;注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求,如果是偶数个则找中间两位数的平均数.


科目:初中数学 来源: 题型:选择题
| A. | 2x2•3x3=6x3 | B. | 2x2+3x3=5x5 | ||
| C. | -12a3b4÷2a3b2=-6b2 | D. | $\frac{5}{4}$xn•$\frac{2}{5}$xm=$\frac{1}{2}$xmn |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 它的图象是一条直线 | B. | 它的图象分布在第一、三象限 | ||
| C. | 点(-1,-5)在它的图象上 | D. | 当x>0时,y随x的增大而增大 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
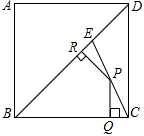 如图,E为边长为2的正方形ABCD的对角线上一点,BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于R,则PQ+PR的值为( )
如图,E为边长为2的正方形ABCD的对角线上一点,BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于R,则PQ+PR的值为( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
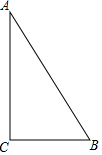 如图,在Rt△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为( )
如图,在Rt△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com