
【题目】抛物线m:y=x2﹣2x+2与直线l:y=x+2交于A,B(A在B的左侧),且抛物线顶点为C.
(1)求A,B,C坐标;
(2)若点D为该抛物线上的一个动点,且在直线AC下方,当以A,C,D为顶点的三角形面积最大时,求点D的坐标及此时三角形的面积.
(3)将抛物线m:y=x2﹣2x+2沿直线OC方向平移得抛物线m′,与直线l:y=x+2交于A′,B′,问在平移过程中线段A′B′的长度是否发生变化,请通过计算说明.
【答案】(1)A(0,2),B(3,5),C(1,1);(2)D(![]() ,
, ![]() );(3)A′B′的长度为定值,理由见解析
);(3)A′B′的长度为定值,理由见解析
【解析】试题分析:(1)利用配方法得到y=(x﹣1)2+1,从而可得到点C的坐标,然后将y=x2﹣2x+2与y=x+2可求得点A和点B的坐标;
(2)过点D作DE∥y轴,交抛物线与点P.先求得直线AC的解析式,设点D的坐标为(m,m2﹣2m+2),则点P的坐标为(m,﹣m+2),则PD=﹣m2+m,然后依据S△ACD=S△APD+S△CPD的到△ACD的面积与m的函数关系式,最后,利用配方法可求解即可.
(3)过点A′作A′M⊥x轴,垂足为M,B′N⊥x轴,垂足为N,作A′G⊥B′N,垂足为G,则A′B′=![]() A′G,设平移后抛物线的解析式为y=(x﹣a)2+a.A′(x1,y1)B′(x2,y2),依据完全平方公式得到A′G=
A′G,设平移后抛物线的解析式为y=(x﹣a)2+a.A′(x1,y1)B′(x2,y2),依据完全平方公式得到A′G=![]() .由将y=x+2代入y=(x﹣a)2+a得到关于x的方程,依据一元二次方程根与系数的关系可得到x2+x1=2a+1,x2x1=a2+a+2,从而可求得A′G的长,最后可得到A′B′的长.
.由将y=x+2代入y=(x﹣a)2+a得到关于x的方程,依据一元二次方程根与系数的关系可得到x2+x1=2a+1,x2x1=a2+a+2,从而可求得A′G的长,最后可得到A′B′的长.
试题解析:(1)∵y=x2﹣2x+2=(x﹣1)2+1,
∴C(1,1),
将y=x2﹣2x+2与y=x+2联立得: ![]() ,解得:
,解得: ![]() 或
或![]() ,
,
∴A(0,2),B(3,5);
(2)如图1所示:过点D作DE∥y轴,交抛物线与点P.
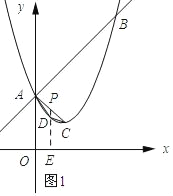
设AC的解析式为y=kx+b,将点A和点C的坐标代入得: ![]() ,解得k=﹣1,b=2,
,解得k=﹣1,b=2,
∴直线AC的解析式为y=﹣x+2,
设点D的坐标为(m,m2﹣2m+2),则点P的坐标为(m,﹣m+2),则PD=(﹣m+2)﹣(m2﹣2m+2)=﹣m2+m.
S△ACD=S△APD+S△CPD=![]() ×1DP=
×1DP=![]() (﹣m2+m)=﹣
(﹣m2+m)=﹣![]() (m﹣
(m﹣![]() )2+
)2+![]() ,
,
∴当m=![]() 时,△ACD的面积有最大值,最大值为
时,△ACD的面积有最大值,最大值为![]() ,
,
此点D的坐标为(![]() ,
, ![]() );
);
(3)如图2所示:过点A′作A′M⊥x轴,垂足为M,B′N⊥x轴,垂足为N,作A′G⊥B′N,垂足为G,则A′B′=![]() A′G,
A′G,
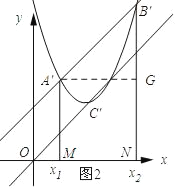
设OC的解析式为y=kx,将点C的坐标代入得到k=1,则OC的解析式为y=x,
设平移后抛物线的解析式为y=(x﹣a)2+a,
设A′(x1,y1)B′(x2,y2),则A′G=|x2﹣x1|=![]() ,
,
将y=x+2代入y=(x﹣a)2+a得:x2﹣(2a+1)x+a2+a+2=0,
∴x2+x1=2a+1,x2x1=a2+a+2.
∴A′G=![]() =3,
=3,
∴A′B′=3![]() ,
,
∴A′B′的长度为定值.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
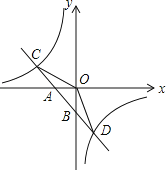
【题目】如图,已知一次函数y1=k1x+b的图象与x轴、y轴分别交于A、B两点,与反比例函数y2=![]() 的图象分别交于C、D两点,点D(2,﹣3),点B是线段AD的中点.
的图象分别交于C、D两点,点D(2,﹣3),点B是线段AD的中点.
(1)求一次函数y1=k1x+b与反比例函数y2=![]() 的解析式;
的解析式;
(2)求△COD的面积;
(3)直接写出![]() 时自变量x的取值范围.
时自变量x的取值范围.
(4)动点P(0,m)在y轴上运动,当![]() 的值最大时,求点P的坐标.
的值最大时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在一次用频率估计概率的实验中,统计了某一结果出现的频率,并绘制了如图所示的统计图,则符合这一结果的实验可能是( )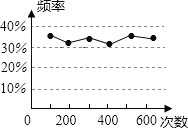
A. 从一个装有2个白球和1个红球的不透明袋子中任意摸出一球(小球除颜色外,完全相同),摸到红球的概率
B. 掷一枚质地均匀的硬币,正面朝上的概率
C. 从一副去掉大小王的扑克牌,任意抽取一张,抽到黑桃的概率
D. 任意买一张电影票,座位号是2的倍数的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.过点A1(1,0)作x轴的垂线,交直线y=2x于点B1;点A2与点O关于直线A1B1对称,过点A2作x轴的垂线,交直线y=2x于点B2;点A3与点O关于直线A2B2对称.过点A3作x轴的垂线,交直线y=2x于点B3;…按此规律作下去.则点A3的坐标为 ,点Bn的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在![]() 中,
中,![]() ,过
,过![]() 上一点
上一点![]() 作
作![]() 交
交![]() 于点
于点![]() ,以
,以![]() 为顶点,
为顶点,![]() 为一边,作
为一边,作![]() ,另一边
,另一边![]() 交
交![]() 于点
于点![]() .
.

(1)求证:四边形![]() 为平行四边形;
为平行四边形;
(2)当点![]() 为
为![]() 中点时,
中点时,![]() 的形状为 ;
的形状为 ;
(3)延长图①中的![]() 到点
到点![]() 使
使![]() 连接
连接![]() 得到图②,若
得到图②,若![]() 判断四边形
判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3, ![]() ),点C的坐标为(
),点C的坐标为(![]() ,0),点P为斜边OB上的一个动点,则PA+PC的最小值为( )
,0),点P为斜边OB上的一个动点,则PA+PC的最小值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
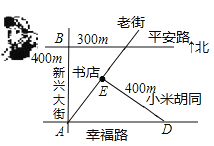
【题目】如图,平安路与幸福路是两条平行的道路,且与新兴大街垂直,老街与小米胡同垂直,书店位于老街与小米胡同的交口处,如果小强同学站在平安路与新兴大街的交叉路口,准备去书店,按图中的街道行走,最近的路程为____________ m.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com