
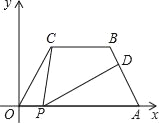
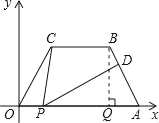
【题目】如图,在平面直角坐标中,四边形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,点P为x轴上的一个动点,但是点P不与点0、点A重合.连接CP,D点是线段AB上一点,连接PD.
(1)求点B的坐标;
(2)当∠CPD=∠OAB,且![]() ,求这时点P的坐标.
,求这时点P的坐标.
【答案】(1) 点B的坐标为(5,![]() );(2) 点P坐标为(1,0)或(6,0).
);(2) 点P坐标为(1,0)或(6,0).
【解析】
(1)依题意可得∠BAQ=∠COA,已知AB=4,∠COA度数利用三角函数可求出BQ,AQ,OQ的值.
(2)利用相似三角形的判定证明△OCP∽△APD,根据等比性质可求出AP,OP的值.
解:(1)作BQ⊥x轴于Q.
∵四边形OABC是等腰梯形,
∴∠BAQ=∠COA=60°
在Rt△BQA中,BA=4,
BQ=ABsin∠BAO=4×sin60°=![]()
AQ=ABcos∠BAO=4×cos60°=2,
∴OQ=OA﹣AQ=7﹣2=5
点B在第一象限内,∴点B的坐标为(5,![]() );
);
(2)∵∠CPA=∠OCP+∠COP,
即∠CPD+∠DPA=∠COP+∠OCP,
而∠CPD=∠OAB=∠COP=60°,
∴∠OCP=∠APD.
∵∠COP=∠PAD,
∴△OCP∽△APD.
∴![]() .
.
∴OPAP=OCAD.
∵![]() ,且AB=4,
,且AB=4,
∴BD=![]() AB=
AB=![]() ,
,
AD=AB﹣BD=4﹣![]() =
=![]() .
.
∵AP=OA﹣OP=7﹣OP,
∴OP(7﹣OP)=4×![]() ,
,
解得:OP=1或6.
∴点P坐标为(1,0)或(6,0).
故答案为:(1) 点B的坐标为(5,![]() );(2) 点P坐标为(1,0)或(6,0).
);(2) 点P坐标为(1,0)或(6,0).


科目:初中数学 来源: 题型:
【题目】抛物线y=x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,﹣3).
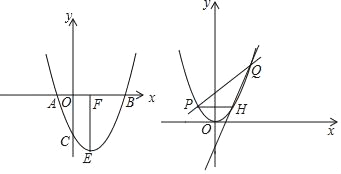
(1)求抛物线的解析式;
(2)如图1,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.
(3)如图2,将抛物线平移,使其顶点E与原点O重合,直线y=kx+2(k>0)与抛物线相交于点P、Q(点P在左边),过点P作x轴平行线交抛物线于点H,当k发生改变时,请说明直线QH过定点,并求定点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一年一度的“春节”即将到来,某超市购进一批价格为每千克3元的桔子,根据市场预测,该种桔子每千克售价4元时,每天能售出500千克,并且售价每上涨0.1元,其销售量将减少10千克,物价部门规定,该种桔子的售价不能超过进价的200%,请你利用所学知识帮助超市给这种桔子定价,使得超市每天销售这种桔子的利润为800元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x﹣3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=﹣x2+mx+n与x轴的另一个交点为A,顶点为P.
(1)求3m+n的值;
(2)在该抛物线的对称轴上是否存在点Q,使以C,P,Q为顶点的三角形为等腰三角形?若存在,求出有符合条件的点Q的坐标;若不存在,请说明理由.
(3)将该抛物线在x轴上方的部分沿x轴向下翻折,图象的其余部分保持不变,翻折后的图象与原图象x轴下方的部分组成一个“M“形状的新图象,若直线y=x+b与该“M”形状的图象部分恰好有三个公共点,求b的值.
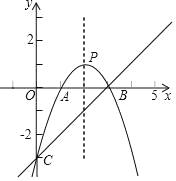
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线x=﹣1的抛物线y=x2+bx+c与x轴相交于A、B两点,其中点A的坐标为(﹣3,0).
(1)求点B的坐标;
(2)求二次函数的解析式;
(3)已知C为抛物线与y轴的交点,设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2m+1)x+m2﹣2=0.
(1)若该方程有两个实数根,求m的最小整数值;
(2)若方程的两个实数根为x1,x2,且(x1﹣x2)2+m2=21,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在抛掷硬币的试验中,下列结论正确的是![]()
![]()
A. 经过大量重复的抛掷硬币试验,可发现“正面向上”的频率越来越稳定
B. 抛掷10000次硬币与抛掷12000次硬币“正面向上”的频率相同
C. 抛掷50000次硬币,可得“正面向上”的频率为![]()
D. 若抛掷2000次硬币“正面向上”的频率是![]() ,则“正面向下”的频率也为
,则“正面向下”的频率也为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个四位正整数s,中间两位均为3,则称这个四位正整数为“三中全会数”;若将这个“三中全会数”的个位与千位交换位置得到新的正整数记为s',并记F(s)=![]()
![]() .例如:F(4331)=
.例如:F(4331)=![]()
![]() .
.
(1)最小的“三中全会数”是 ;F(2331)= ;
(2)若“三中全会数”的个位与千位数字恰好相同,则又称这个四位正整数为“三中对称数”,若“三中全会数”x,y中x恰好是“三中对称数”,且F(x)能被11整除;F(y)﹣2F(x)=31,求出“三中全会数”y的所有可能值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在研究“利用木板余料裁出最大面积的矩形”时发现:如图1,![]() 是一块直角三角形形状的木板余料
是一块直角三角形形状的木板余料![]() ,以
,以![]() 为内角裁一个矩形当DE,EF是中位线时,所裁矩形的面积最大
为内角裁一个矩形当DE,EF是中位线时,所裁矩形的面积最大![]() 若木板余料的形状改变,请你探究:
若木板余料的形状改变,请你探究:
![]() 如图2,现有一块五边形的木板余料ABCDE,
如图2,现有一块五边形的木板余料ABCDE,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 现从中裁出一个以
现从中裁出一个以![]() 为内角且面积最大的矩形,则该矩形的面积为______
为内角且面积最大的矩形,则该矩形的面积为______![]() .
.
![]() 如图3,现有一块四边形的木板余料ABCD,经测量
如图3,现有一块四边形的木板余料ABCD,经测量![]() ,
,![]() ,
,![]() ,且
,且![]() ,从中裁出顶点M,N在边BC上且面积最大的矩形PQMN,则该矩形的面积为______
,从中裁出顶点M,N在边BC上且面积最大的矩形PQMN,则该矩形的面积为______![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com