
【题目】若一个四位正整数s,中间两位均为3,则称这个四位正整数为“三中全会数”;若将这个“三中全会数”的个位与千位交换位置得到新的正整数记为s',并记F(s)=![]()
![]() .例如:F(4331)=
.例如:F(4331)=![]()
![]() .
.
(1)最小的“三中全会数”是 ;F(2331)= ;
(2)若“三中全会数”的个位与千位数字恰好相同,则又称这个四位正整数为“三中对称数”,若“三中全会数”x,y中x恰好是“三中对称数”,且F(x)能被11整除;F(y)﹣2F(x)=31,求出“三中全会数”y的所有可能值.
【答案】(1)1331,333 ;(2)2333,3332,1334,4331.
【解析】
(1)最小的“三中全会数”是个位和千位的数字都最小即可;F(2331)根据式子可以直接进行计算;
(2)根据题目已知条件,即可表示出F(x),即可算出F(x),然后根据F(y)﹣2F(x)=31,即可求出F(y),根据“三中全会数”即可求出y的所有值.
解:(1)最小的三中全会数是1330,F(2331)=![]() =333;
=333;
故答案为:1331;333.
(2)设x的个位和千位的数字是a,则F(x)=![]() ,且F(x)能被11整除,故a=1.
,且F(x)能被11整除,故a=1.
∴F(x)=242,代入F(y)﹣2F(x)=31.
∴F(y)=515.y+y′=515×11=5665,及y的值为:2333,3332,1334,4331.
故“三中全会数”y的所有可能值有:2333,3332,1334,4331.


科目:初中数学 来源: 题型:
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=m.若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),则花园面积S的最大值为( )
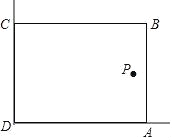
A. 193 B. 194 C. 195 D. 196
查看答案和解析>>
科目:初中数学 来源: 题型:
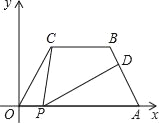
【题目】如图,在平面直角坐标中,四边形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,点P为x轴上的一个动点,但是点P不与点0、点A重合.连接CP,D点是线段AB上一点,连接PD.
(1)求点B的坐标;
(2)当∠CPD=∠OAB,且![]() ,求这时点P的坐标.
,求这时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批衬衫,平均每天可售出20件,每件盈利40元![]() 为了扩大销售,增加盈利,商场决定采取降价措施,经调查发现,若毎件衬衫每降价1元,商场平均每天可多售出2件.
为了扩大销售,增加盈利,商场决定采取降价措施,经调查发现,若毎件衬衫每降价1元,商场平均每天可多售出2件.
![]() 若每件降价x元,每天盈利y元,求出y与x之间的关系式;
若每件降价x元,每天盈利y元,求出y与x之间的关系式;
![]() 每件衬衫降价多少元时,商场每天盈利最多?盈利多少元?
每件衬衫降价多少元时,商场每天盈利最多?盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两地之间有一条直线跑道,甲,乙两人分别从A,B同时出发,相向而行匀速跑步,且乙的速度是甲速度的80%,当甲,乙分别到达B地,A地后立即调头往回跑,甲的速度保持不变,乙的速度提高25%(仍保持匀速前行),甲,乙两人之间的距离y(米)与跑步时间x(分钟)之间的关系如图所示,则他们在第二次相遇时距B地_____米.
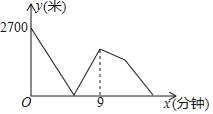
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半圆O的直径![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,半圆O以
,半圆O以![]() 的速度从左向右运动,在运动过程中,点D、E始终在直线BC上,设运动时间为
的速度从左向右运动,在运动过程中,点D、E始终在直线BC上,设运动时间为![]() ,当
,当![]() 时,半圆O在
时,半圆O在![]() 的左侧,
的左侧,![]() .
.
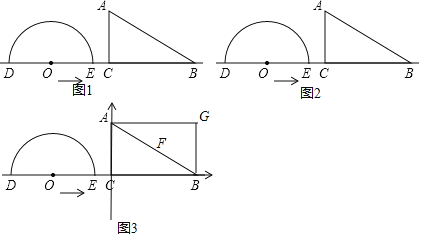
![]() 如图1当
如图1当![]() 时,圆心O到AB所在直线的距离是______cm.
时,圆心O到AB所在直线的距离是______cm.
![]() 当t为何值时,
当t为何值时,![]() 的边AB所在的直线与半圆O所在圆相切?求时间t.
的边AB所在的直线与半圆O所在圆相切?求时间t.
![]() 如图2,线段AB的中点为F,求圆心O与B、F两点构成以BF为腰的等腰三角形时运动的时间t.
如图2,线段AB的中点为F,求圆心O与B、F两点构成以BF为腰的等腰三角形时运动的时间t.
![]() 在图2的基础上,建立如图所示的平面直角坐标系,四边形ACBG是矩形,如图3,半圆O向右运动的同时矩形也向右运动,速度为
在图2的基础上,建立如图所示的平面直角坐标系,四边形ACBG是矩形,如图3,半圆O向右运动的同时矩形也向右运动,速度为![]() ,问经过多长时间O、F、G在同一条直线上,求时间
,问经过多长时间O、F、G在同一条直线上,求时间![]() 并求出此时DG的直线解析式.
并求出此时DG的直线解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是![]()
![]()

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量是售价的一次函数,且相关信息如下表:
售价(元/件) | 100 | 110 | 120 | 130 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元,设售价为x元.
(1)请用含x的式子表示:①销售该运动服每件的利润是( )元;
(2)求月销量y与售价x的一次函数关系式:
(3)设销售该运动服的月利润为W元,那么售价为多少元时,当月的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有四张背面完全相同的纸牌![]() ,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.
,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.
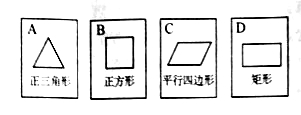
(1)从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形小明获胜,否则小亮获胜,这个游戏公平吗?请用列表法(或树状图)说明理由(纸牌用![]() 表示).
表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com