
°æƒø°ø»ÁÕº£¨∞Α≤Oµƒ÷±æ∂![]() £¨‘⁄
£¨‘⁄![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨![]() £¨∞Α≤O“‘
£¨∞Α≤O“‘![]() µƒÀŸ∂»¥”◊ۜڔ“‘À∂Ø£¨‘⁄‘À∂Øπ˝≥Ã÷–£¨µ„D°¢E º÷’‘⁄÷±œþBC…œ£¨…Ë‘À∂Ø ±º‰Œ™
µƒÀŸ∂»¥”◊ۜڔ“‘À∂Ø£¨‘⁄‘À∂Øπ˝≥Ã÷–£¨µ„D°¢E º÷’‘⁄÷±œþBC…œ£¨…Ë‘À∂Ø ±º‰Œ™![]() £¨µ±
£¨µ±![]() ±£¨∞Α≤O‘⁄
±£¨∞Α≤O‘⁄![]() µƒ◊Û≤ý£¨
µƒ◊Û≤ý£¨![]() £Æ
£Æ
![]() »ÁÕº1µ±
»ÁÕº1µ±![]() ±£¨‘≤–ƒOµΩABÀ˘‘⁄÷±œþµƒæý¿Î «______cm£Æ
±£¨‘≤–ƒOµΩABÀ˘‘⁄÷±œþµƒæý¿Î «______cm£Æ
![]() µ±tŒ™∫Œ÷µ ±£¨
µ±tŒ™∫Œ÷µ ±£¨![]() µƒ±þABÀ˘‘⁄µƒ÷±œþ”Î∞Α≤OÀ˘‘⁄‘≤œý«–£ø«Û ±º‰t£Æ
µƒ±þABÀ˘‘⁄µƒ÷±œþ”Î∞Α≤OÀ˘‘⁄‘≤œý«–£ø«Û ±º‰t£Æ
![]() »ÁÕº2£¨œþ∂ŒABµƒ÷–µ„Œ™F£¨«Û‘≤–ƒO”ÎB°¢F¡Ωµ„ππ≥…“‘BFŒ™—¸µƒµ»—¸»˝Ω«–Œ ±‘À∂صƒ ±º‰t£Æ
»ÁÕº2£¨œþ∂ŒABµƒ÷–µ„Œ™F£¨«Û‘≤–ƒO”ÎB°¢F¡Ωµ„ππ≥…“‘BFŒ™—¸µƒµ»—¸»˝Ω«–Œ ±‘À∂صƒ ±º‰t£Æ
![]() ‘⁄Õº2µƒª˘¥°…œ£¨Ω®¡¢»ÁÕºÀ˘ 浃∆Ω√Ê÷±Ω«◊¯±Íœµ£¨Àƒ±þ–ŒACBG «æÿ–Œ£¨»ÁÕº3£¨∞Α≤OœÚ”“‘À∂صƒÕ¨ ±æÿ–Œ“≤œÚ”“‘À∂Ø£¨ÀŸ∂»Œ™
‘⁄Õº2µƒª˘¥°…œ£¨Ω®¡¢»ÁÕºÀ˘ 浃∆Ω√Ê÷±Ω«◊¯±Íœµ£¨Àƒ±þ–ŒACBG «æÿ–Œ£¨»ÁÕº3£¨∞Α≤OœÚ”“‘À∂صƒÕ¨ ±æÿ–Œ“≤œÚ”“‘À∂Ø£¨ÀŸ∂»Œ™![]() £¨Œ æ≠π˝∂ý≥§ ±º‰O°¢F°¢G‘⁄Õ¨“ªÃı÷±œþ…œ£¨«Û ±º‰
£¨Œ æ≠π˝∂ý≥§ ±º‰O°¢F°¢G‘⁄Õ¨“ªÃı÷±œþ…œ£¨«Û ±º‰![]() ≤¢«Û≥ˆ¥À ±DGµƒ÷±œþΩ‚Œˆ Ω£Æ
≤¢«Û≥ˆ¥À ±DGµƒ÷±œþΩ‚Œˆ Ω£Æ
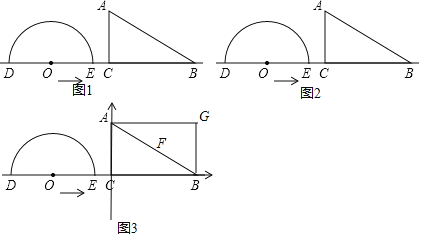
°æ¥∞∏°ø£®1£©9£ª£®2£©µ±![]() ªÚ32s ±£¨AB”Î∞Α≤OÀ˘‘⁄µƒ‘≤œý«–£ª£®3£©¬˙◊„Ãıº˛µƒtµƒ÷µŒ™
ªÚ32s ±£¨AB”Î∞Α≤OÀ˘‘⁄µƒ‘≤œý«–£ª£®3£©¬˙◊„Ãıº˛µƒtµƒ÷µŒ™![]() £¨
£¨![]() £¨
£¨![]() £ª£®4£©
£ª£®4£©![]() £Æ
£Æ
°æΩ‚Œˆ°ø
£®1£©µ±t=2 ±£¨µ„E”ε„C÷ÿ∫œ£¨»ÁÕº1÷–£¨◊˜OH°ÕAB”⁄H£ÆΩ‚÷±Ω«»˝Ω«–Œ«Û≥ˆOHº¥ø…£ª
£®2£©∑÷¡Ω÷÷«È–Œ¢Ÿ»ÁÕº2÷–£¨π˝Cµ„◊˜CF°ÕAB£¨ΩªAB”⁄Fµ„£ª¢⁄µ±µ„O‘À∂صΩBµ„µƒ”“≤ý£¨«“OB=12cm ±£¨»ÁÕº3÷–£¨π˝µ„O◊˜OQ°Õ÷±œþAB£¨¥π◊„Œ™Q£Æ∑÷±«ÛΩ‚º¥ø…£ª
£®3£©¢Ÿµ±µ„O”ÎC÷ÿ∫œ ±£¨°˜BOF «µ»—¸»˝Ω«–Œ£¨¥À ±t=8£ª¢⁄µ±BF=BO ±£¨‘⁄Rt°˜ABC÷–£¨![]() £¨Õ∆≥ˆBO°‰=4
£¨Õ∆≥ˆBO°‰=4![]() ªÚBO°Â=4
ªÚBO°Â=4![]() ±£¨°˜OBF «µ»—¸»˝Ω«–Œ£¨”…¥Àº¥ø…Ω‚æˆŒ £ª
±£¨°˜OBF «µ»—¸»˝Ω«–Œ£¨”…¥Àº¥ø…Ω‚æˆŒ £ª
£®4£©t√Î∫Û£¨G£®12+0.5t£¨4![]() £©£¨F£®6+0.5t£¨2
£©£¨F£®6+0.5t£¨2![]() £©£¨O£®-8+t£¨0£©£¨µ±O°¢F°¢Gπ≤œþ ±£¨µ„F «O°¢Gµƒ÷–µ„£¨‘Ú”–
£©£¨O£®-8+t£¨0£©£¨µ±O°¢F°¢Gπ≤œþ ±£¨µ„F «O°¢Gµƒ÷–µ„£¨‘Ú”–![]() =6+0.5t£¨«Û≥ˆtº¥ø…Ω‚æˆŒ £ª
=6+0.5t£¨«Û≥ˆtº¥ø…Ω‚æˆŒ £ª
Ω‚£∫![]() »ÁÕº1÷–£¨◊˜
»ÁÕº1÷–£¨◊˜![]() ”⁄H£Æ
”⁄H£Æ
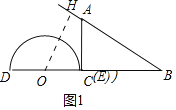
µ±![]() ±£¨µ„E”ε„C÷ÿ∫œ£¨
±£¨µ„E”ε„C÷ÿ∫œ£¨![]() £¨
£¨
‘⁄![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨
![]() £Æ
£Æ
π ¥∞∏Œ™9£Æ
![]() »ÁÕº2÷–£¨π˝Cµ„◊˜
»ÁÕº2÷–£¨π˝Cµ„◊˜![]() £¨ΩªAB”⁄Fµ„£ª
£¨ΩªAB”⁄Fµ„£ª
![]() £¨
£¨![]() £¨
£¨
![]() £ª
£ª
µ±∞Α≤O”Î![]() µƒ±þABœý«– ±£¨
µƒ±þABœý«– ±£¨
”÷![]() ‘≤–ƒOµΩABµƒæý¿Îµ»”⁄6cm£¨
‘≤–ƒOµΩABµƒæý¿Îµ»”⁄6cm£¨
«“‘≤–ƒO”÷‘⁄÷±œþBC…œ£¨
![]() ”ÎC÷ÿ∫œ£¨
”ÎC÷ÿ∫œ£¨
º¥µ±Oµ„‘À∂صΩCµ„ ±£¨∞Α≤O”Î![]() µƒ±þABœý«–£ª
µƒ±þABœý«–£ª
¥À ±µ„O‘À∂Ø¡À8cm£¨À˘«Û‘À∂Ø ±º‰Œ™![]() £¨
£¨
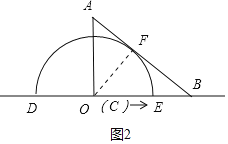
![]() µ±µ„O‘À∂صΩBµ„µƒ”“≤ý£¨«“
µ±µ„O‘À∂صΩBµ„µƒ”“≤ý£¨«“![]() ±£¨»ÁÕº3÷–£¨π˝µ„O◊˜
±£¨»ÁÕº3÷–£¨π˝µ„O◊˜![]() ÷±œþAB£¨¥π◊„Œ™Q£Æ
÷±œþAB£¨¥π◊„Œ™Q£Æ
‘⁄![]() ÷–£¨
÷–£¨![]() £¨‘Ú
£¨‘Ú![]() £¨
£¨
º¥OQ”Î∞Α≤OÀ˘‘⁄µƒ‘≤œý«–![]() ¥À ±µ„O‘À∂Ø¡À32cm£Æ
¥À ±µ„O‘À∂Ø¡À32cm£Æ
À˘«Û‘À∂Ø ±º‰Œ™£∫![]() £¨
£¨
◊€…œø…÷™µ±![]() ªÚ32s ±£¨AB”Î∞Α≤OÀ˘‘⁄µƒ‘≤œý«–£ª
ªÚ32s ±£¨AB”Î∞Α≤OÀ˘‘⁄µƒ‘≤œý«–£ª
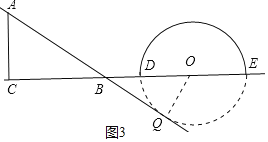
![]() »ÁÕº4÷–£¨
»ÁÕº4÷–£¨
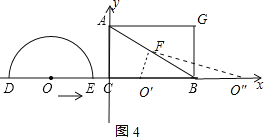
![]() µ±µ„O”ÎC÷ÿ∫œ ±£¨
µ±µ„O”ÎC÷ÿ∫œ ±£¨![]() «µ»—¸»˝Ω«–Œ£¨¥À ±
«µ»—¸»˝Ω«–Œ£¨¥À ±![]() £ª
£ª
![]() µ±
µ±![]() ±£¨‘⁄
±£¨‘⁄![]() ÷–£¨
÷–£¨![]() £¨
£¨
![]() ªÚ
ªÚ![]() ±£¨
±£¨![]() «µ»—¸»˝Ω«–Œ£¨
«µ»—¸»˝Ω«–Œ£¨
¥À ±![]() ªÚ
ªÚ![]()
◊€…œÀ˘ ˆ£¨¬˙◊„Ãıº˛µƒtµƒ÷µŒ™![]() £¨
£¨![]() £¨
£¨![]() £ª
£ª
![]() √Î∫Û£¨
√Î∫Û£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨
µ±O°¢F°¢Gπ≤œþ ±£¨µ„F «O°¢Gµƒ÷–µ„£¨
‘Ú”–![]() £¨
£¨
Ω‚µ√![]() £¨
£¨
¥À ±![]() £¨
£¨![]() £¨
£¨
…Ë÷±œþDGµƒΩ‚Œˆ ΩŒ™![]() £¨
£¨
‘Ú![]() £¨Ω‚µ√
£¨Ω‚µ√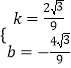
![]() £Æ
£Æ


 ‘∆ƒœ ¶¥Û∏Ω–°“ªœþ√˚ ¶Ã·”≈◊˜“µœµ¡–¥∞∏
‘∆ƒœ ¶¥Û∏Ω–°“ªœþ√˚ ¶Ã·”≈◊˜“µœµ¡–¥∞∏ ≥Â¥Ã100∑÷µ•‘™”≈ªØ¡∑øºæÌœµ¡–¥∞∏
≥Â¥Ã100∑÷µ•‘™”≈ªØ¡∑øºæÌœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™£∫»ÁÕº1£¨≈◊ŒÔœþµƒ∂•µ„Œ™M£¨∆Ω––”⁄x÷·µƒ÷±œþ”Î∏√≈◊ŒÔœþΩª”⁄µ„A£¨B£®µ„A‘⁄µ„B◊Û≤ý£©£¨∏˘æð∂‘≥∆–‘°˜AMB∫„Œ™µ»—¸»˝Ω«–Œ£¨Œ“√«πÊ∂®£∫µ±°˜AMBŒ™÷±Ω«»˝Ω«–Œ ±£¨æÕ≥∆°˜AMBŒ™∏√≈◊ŒÔœþµƒ°∞ÕÍ√¿»˝Ω«–Œ°±£Æ

£®1£©¢Ÿ»ÁÕº2£¨«Û≥ˆ≈◊ŒÔœþ![]() µƒ°∞ÕÍ√¿»˝Ω«–Œ°±–±±þABµƒ≥§£ª
µƒ°∞ÕÍ√¿»˝Ω«–Œ°±–±±þABµƒ≥§£ª
¢⁄≈◊ŒÔœþ![]() ”Î
”Î![]() µƒ°∞ÕÍ√¿»˝Ω«–Œ°±µƒ–±±þ≥§µƒ ˝¡øπÿœµ « £ª
µƒ°∞ÕÍ√¿»˝Ω«–Œ°±µƒ–±±þ≥§µƒ ˝¡øπÿœµ « £ª
£®2£©»Ù≈◊ŒÔœþ![]() µƒ°∞ÕÍ√¿»˝Ω«–Œ°±µƒ–±±þ≥§Œ™4£¨«Ûaµƒ÷µ£ª
µƒ°∞ÕÍ√¿»˝Ω«–Œ°±µƒ–±±þ≥§Œ™4£¨«Ûaµƒ÷µ£ª
£®3£©»Ù≈◊ŒÔœþ![]() µƒ°∞ÕÍ√¿»˝Ω«–Œ°±–±±þ≥§Œ™n£¨«“
µƒ°∞ÕÍ√¿»˝Ω«–Œ°±–±±þ≥§Œ™n£¨«“![]() µƒ◊Ó¥Û÷µŒ™-1£¨«Ûm£¨nµƒ÷µ£Æ
µƒ◊Ó¥Û÷µŒ™-1£¨«Ûm£¨nµƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™πÿ”⁄xµƒ“ª‘™∂˛¥Œ∑Ω≥Ãx2+£®2m+1£©x+m2©Å2=0£Æ
£®1£©»Ù∏√∑Ω≥Ô–¡Ω∏ˆ µ ˝∏˘£¨«Ûmµƒ◊Ó–°’˚ ˝÷µ£ª
£®2£©»Ù∑Ω≥õƒ¡Ω∏ˆ µ ˝∏˘Œ™x1£¨x2£¨«“£®x1©Åx2£©2+m2=21£¨«Ûmµƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
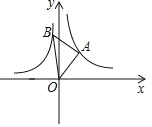
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨µ»—¸Rt°˜ABOµƒ∂•µ„A£¨B∑÷±‘⁄∑¥±»¿˝∫Ø ˝y£Ω![]() £®k£æ0£©”Îy£Ω©Å
£®k£æ0£©”Îy£Ω©Å![]()
![]() …œ£¨«“Aµ„µƒ∫·◊¯±ÍŒ™2£¨‘Úkµƒ÷µŒ™£®°°°°£©
…œ£¨«“Aµ„µƒ∫·◊¯±ÍŒ™2£¨‘Úkµƒ÷µŒ™£®°°°°£©
A. ![]() B.
B. ![]() C. 1D. 1+
C. 1D. 1+![]()
![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»Ù“ª∏ˆÀƒŒª’˝’˚ ˝s£¨÷–º‰¡ΩŒªæ˘Œ™3£¨‘Ú≥∆’‚∏ˆÀƒŒª’˝’˚ ˝Œ™°∞»˝÷–»´ª· ˝°±£ª»ÙΩ´’‚∏ˆ°∞»˝÷–»´ª· ˝°±µƒ∏ˆŒª”ΫߌªΩªªªŒª÷√µ√µΩ–¬µƒ’˝’˚ ˝º«Œ™s'£¨≤¢º«F£®s£©£Ω![]()
![]() £Æ¿˝»Á£∫F£®4331£©£Ω
£Æ¿˝»Á£∫F£®4331£©£Ω![]()
![]() £Æ
£Æ
£®1£©◊Ó–°µƒ°∞»˝÷–»´ª· ˝°± «°° °°£ªF£®2331£©£Ω°° °°£ª
£®2£©»Ù°∞»˝÷–»´ª· ˝°±µƒ∏ˆŒª”Ϋߌª ˝◊÷«°∫√œýÕ¨£¨‘Ú”÷≥∆’‚∏ˆÀƒŒª’˝’˚ ˝Œ™°∞»˝÷–∂‘≥∆ ˝°±£¨»Ù°∞»˝÷–»´ª· ˝°±x£¨y÷–x«°∫√ «°∞»˝÷–∂‘≥∆ ˝°±£¨«“F£®x£©ƒÐ±ª11’˚≥˝£ªF£®y£©©Å2F£®x£©£Ω31£¨«Û≥ˆ°∞»˝÷–»´ª· ˝°±yµƒÀ˘”–ø…ƒÐ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄“ª¥Œπ„≥°ŒË±»»¸÷–£¨º◊°¢““¡Ω∏ˆ∂”≤Œº”±Ì—ðµƒ≈Ɨ𑱵ƒ…Ì∏þ£®µ•Œª£∫cm£©∑÷± «£∫
º◊∂” 163 164 165 165 165 165 166 167
““∂” 162 164 164 165 165 166 167 167
£®1£©«Ûº◊∂”≈Ɨ𑱅Ì∏þµƒ∆Ωæ˘ ˝°¢÷–Œª ˝°¢÷⁄ ˝£ª
£®2£©ƒƒ∏ˆ∂”≈Ɨ𑱵ƒ…Ì∏þ∏¸’˚∆Σø«Î¥”∑Ω≤ÓµƒΩ«∂»Àµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™£∫‘⁄![]() ÷–£¨C°¢D∑÷±Œ™BM°¢AM…œµƒµ„£¨Àƒ±þ–ŒABCDƒ⁄Ω””⁄
÷–£¨C°¢D∑÷±Œ™BM°¢AM…œµƒµ„£¨Àƒ±þ–ŒABCDƒ⁄Ω””⁄![]() £¨¡¨Ω”AC£¨
£¨¡¨Ω”AC£¨![]() £ª
£ª
![]() »ÁÕº
»ÁÕº![]() £¨«Û÷§£∫ª°
£¨«Û÷§£∫ª°![]() ª°BD£ª
ª°BD£ª
![]() »ÁÕº
»ÁÕº![]() £¨»ÙABŒ™÷±æ∂£¨
£¨»ÙABŒ™÷±æ∂£¨![]() £¨«Û
£¨«Û![]() ÷µ£ª
÷µ£ª
![]() »ÁÕº
»ÁÕº![]() £¨‘⁄
£¨‘⁄![]() µƒÃıº˛œ¬£¨EŒ™ª°CD…œ“ªµ„
µƒÃıº˛œ¬£¨EŒ™ª°CD…œ“ªµ„![]() ≤ª”ÎC°¢D÷ÿ∫œ
≤ª”ÎC°¢D÷ÿ∫œ![]() £¨FŒ™AB…œ“ªµ„£¨¡¨Ω”EFΩªAC”⁄µ„N£¨¡¨Ω”DN°¢DE£¨»Ù
£¨FŒ™AB…œ“ªµ„£¨¡¨Ω”EFΩªAC”⁄µ„N£¨¡¨Ω”DN°¢DE£¨»Ù![]() £¨
£¨![]() £¨
£¨![]() £¨«ÛANµƒ≥§£Æ
£¨«ÛANµƒ≥§£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“‚¥Û¿˚÷¯√˚ ˝—ߺ“Ï≥≤®ƒ«∆ı‘⁄—–æøÕ√◊”∑±÷≥Œ  ±£¨∑¢œ÷”–’‚—˘“ª◊È ˝£∫1£¨1£¨2£¨3£¨5£¨8£¨13£¨°≠£¨∆‰÷–¥”µ⁄»˝∏ˆ ˝∆£¨√ø“ª∏ˆ ˝∂ºµ»”⁄À¸«∞√Ê¡Ω∏ˆ ˝µƒ∫գƜ÷“‘’‚◊È ˝÷–µƒ∏˜∏ˆ ˝◊˜Œ™’˝∑Ω–Œµƒ±þ≥§÷µππ‘Ï’˝∑Ω–Œ£¨‘Ÿ∑÷±“¿¥Œ¥”◊ÛµΩ”“»°2∏ˆ°¢3∏ˆ°¢4∏ˆ°¢5∏ˆ°≠’˝∑Ω–Œ∆¥≥…»Á…œ≥§∑Ω–Œ£¨»Ù∞¥¥Àπʬ…ºÃ–¯◊˜≥§∑Ω–Œ£¨‘Ú–Ú∫≈Œ™¢þµƒ≥§∑Ω–Œ÷Ð≥§ « £Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
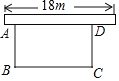
°æƒø°øŒ™œÏ”¶æ£÷ð –°∞¥¥Ω®»´π˙Œƒ√˜≥« –°±∫≈’Ÿ£¨ƒ≥µ•Œª≤ª∂œ√¿ªØª∑æ≥£¨ƒ‚‘⁄“ªøÈæÿ–Œø’µÿ…œ–ÞΩ®¬Ã…´÷≤ŒÔ‘∞£¨∆‰÷–“ª±þøø«Ω£¨ø…¿˚”√µƒ«Ω≥§≤ª≥¨π˝18m£¨¡ÌÕ‚»˝±þ”…36m≥§µƒ’§¿∏Œß≥…£Æ…Ëæÿ–ŒABCDø’µÿ÷–£¨¥π÷±”⁄«Ωµƒ±þAB=xm£¨√ʪ˝Œ™ym2£®»ÁÕº£©£Æ
£®1£©«Ûy”Îx÷ƺ‰µƒ∫Ø ˝πÿœµ Ω£¨≤¢–¥≥ˆ◊‘±‰¡øxµƒ»°÷µ∑∂Œß£ª
£®2£©»Ùæÿ–Œø’µÿµƒ√ʪ˝Œ™160m2£¨«Ûxµƒ÷µ£ª
£®3£©»Ù∏√µ•Œª”√8600‘™π∫¬Ú¡Àº◊°¢““°¢±˚»˝÷÷¬Ã…´÷≤ŒÔπ≤400ø√£®√ø÷÷÷≤ŒÔµƒµ•º€∫Õ√øø√‘‘÷÷µƒ∫œ¿Ì”√µÿ√ʪ˝»Áœ¬±Ì£©£ÆŒ ±˚÷÷÷≤ŒÔ◊Ó∂ýø…“‘π∫¬Ú∂ý…Ÿø√£ø¥À ±£¨’‚≈˙÷≤ŒÔø…“‘»´≤ø‘‘÷÷µΩ’‚øÈø’µÿ…œ¬£ø«ÎÀµ√˜¿Ì”…£Æ
º◊ | ““ | ±˚ | |
µ•º€£®‘™/ø√£© | 14 | 16 | 28 |
∫œ¿Ì”√µÿ£®m2/ø√£© | 0.4 | 1 | 0.4 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com