
【题目】已知:在![]() 中,C、D分别为BM、AM上的点,四边形ABCD内接于
中,C、D分别为BM、AM上的点,四边形ABCD内接于![]() ,连接AC,
,连接AC,![]() ;
;
![]() 如图
如图![]() ,求证:弧
,求证:弧![]() 弧BD;
弧BD;
![]() 如图
如图![]() ,若AB为直径,
,若AB为直径,![]() ,求
,求![]() 值;
值;
![]() 如图
如图![]() ,在
,在![]() 的条件下,E为弧CD上一点
的条件下,E为弧CD上一点![]() 不与C、D重合
不与C、D重合![]() ,F为AB上一点,连接EF交AC于点N,连接DN、DE,若
,F为AB上一点,连接EF交AC于点N,连接DN、DE,若![]() ,
,![]() ,
,![]() ,求AN的长.
,求AN的长.

【答案】(1)详见解析;(2)![]() (3)
(3)![]()
【解析】
![]() 证明弧
证明弧![]() 弧BD可以转化证明
弧BD可以转化证明![]()
![]() 是直径可知三角形ABD是等腰直角三角形,从而得出
是直径可知三角形ABD是等腰直角三角形,从而得出![]() ,利用
,利用![]() 的特殊性构造直角三角形DCG,结合
的特殊性构造直角三角形DCG,结合![]() ,可以求出
,可以求出![]() ,进而求出
,进而求出![]()
![]() 为了求AN,可以过点N作
为了求AN,可以过点N作![]() 于点M,求出MN,AM,即可求出
于点M,求出MN,AM,即可求出![]() 因为P是BD的中点,所以连结OP,根据垂径定理可以得出
因为P是BD的中点,所以连结OP,根据垂径定理可以得出![]() ,根据
,根据![]() 可得
可得![]() ,从而得到矩形OPLH,结合矩形的性质,可以得出OH,EH的长度关系,在利用勾股定理建立方程,可求出HO,进而求出MN,AM,最终得出AN的长度.
,从而得到矩形OPLH,结合矩形的性质,可以得出OH,EH的长度关系,在利用勾股定理建立方程,可求出HO,进而求出MN,AM,最终得出AN的长度.
![]() ,
,![]()
![]() ,
,
又![]()
![]() ,
,
![]() 弧
弧![]() 弧BD
弧BD
![]() 作
作![]() 于点G,连结
于点G,连结![]() 如图
如图![]()
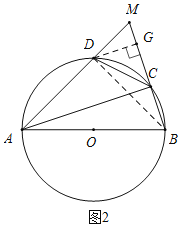
![]() 为直径
为直径
弧![]() 弧
弧![]()
![]() ,
,
又![]()
![]() ,
,
又![]()
![]() ,
,
![]() 连结BD交AC,EF分别为点P,点L,连结OP,OE,PE,再作
连结BD交AC,EF分别为点P,点L,连结OP,OE,PE,再作![]() 于点H,
于点H,![]() 于点
于点![]() 如图3所示
如图3所示![]()
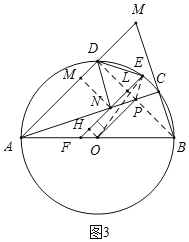
![]() ,
,![]() ,
,
![]() ,
,
由![]() 得
得![]()
![]() ,
,
即P为BD的中点
![]() ,
,
![]() 四边形OPLH为矩形
四边形OPLH为矩形
设![]() ,则
,则![]() .
.
又![]()
![]() 垂直平分NE
垂直平分NE
![]() ,
,
又![]() 为等腰直角三角形
为等腰直角三角形
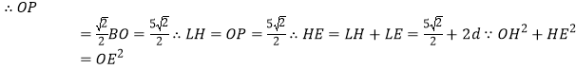
![]() ,
,
解得![]()
![]() ,
,
![]() .
.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】自2016年国庆后,许多高校均投放了使用手机就可随用的共享单车.某运营商为提高其经营的A品牌共享单车的市场占有率,准备对收费作如下调整:一天中,同一个人第一次使用的车费按0.5元收取,每增加一次,当次车费就比上次车费减少0.1元,第6次开始,当次用车免费.具体收费标准如下:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5(含5次以上) |
累计车费 | 0 | 0.5 | 0.9 |
|
| 1.5 |
同时,就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿,得到如下数据:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 5 | 15 | 10 | 30 | 25 | 15 |
(Ⅰ)写出![]() 的值;
的值;
(Ⅱ)已知该校有5000名师生,且A品牌共享单车投放该校一天的费用为5800元.试估计:收费调整后,此运营商在该校投放A品牌共享单车能否获利? 说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批衬衫,平均每天可售出20件,每件盈利40元![]() 为了扩大销售,增加盈利,商场决定采取降价措施,经调查发现,若毎件衬衫每降价1元,商场平均每天可多售出2件.
为了扩大销售,增加盈利,商场决定采取降价措施,经调查发现,若毎件衬衫每降价1元,商场平均每天可多售出2件.
![]() 若每件降价x元,每天盈利y元,求出y与x之间的关系式;
若每件降价x元,每天盈利y元,求出y与x之间的关系式;
![]() 每件衬衫降价多少元时,商场每天盈利最多?盈利多少元?
每件衬衫降价多少元时,商场每天盈利最多?盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半圆O的直径![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,半圆O以
,半圆O以![]() 的速度从左向右运动,在运动过程中,点D、E始终在直线BC上,设运动时间为
的速度从左向右运动,在运动过程中,点D、E始终在直线BC上,设运动时间为![]() ,当
,当![]() 时,半圆O在
时,半圆O在![]() 的左侧,
的左侧,![]() .
.
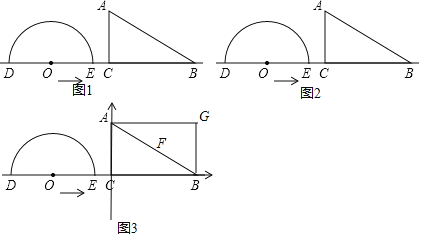
![]() 如图1当
如图1当![]() 时,圆心O到AB所在直线的距离是______cm.
时,圆心O到AB所在直线的距离是______cm.
![]() 当t为何值时,
当t为何值时,![]() 的边AB所在的直线与半圆O所在圆相切?求时间t.
的边AB所在的直线与半圆O所在圆相切?求时间t.
![]() 如图2,线段AB的中点为F,求圆心O与B、F两点构成以BF为腰的等腰三角形时运动的时间t.
如图2,线段AB的中点为F,求圆心O与B、F两点构成以BF为腰的等腰三角形时运动的时间t.
![]() 在图2的基础上,建立如图所示的平面直角坐标系,四边形ACBG是矩形,如图3,半圆O向右运动的同时矩形也向右运动,速度为
在图2的基础上,建立如图所示的平面直角坐标系,四边形ACBG是矩形,如图3,半圆O向右运动的同时矩形也向右运动,速度为![]() ,问经过多长时间O、F、G在同一条直线上,求时间
,问经过多长时间O、F、G在同一条直线上,求时间![]() 并求出此时DG的直线解析式.
并求出此时DG的直线解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是![]()
![]()

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).

(1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)请画出△ABC绕点B逆时针旋转90°后的△A2BC2;
(3)求出(2)中C点旋转到C2点所经过的路径长(记过保留根号和π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量是售价的一次函数,且相关信息如下表:
售价(元/件) | 100 | 110 | 120 | 130 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元,设售价为x元.
(1)请用含x的式子表示:①销售该运动服每件的利润是( )元;
(2)求月销量y与售价x的一次函数关系式:
(3)设销售该运动服的月利润为W元,那么售价为多少元时,当月的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知![]() ,
,![]() ,点P为AB边上的一个动点,点E、F分别是CA,CB边的中点,过点P作
,点P为AB边上的一个动点,点E、F分别是CA,CB边的中点,过点P作![]() 于D,设
于D,设![]() ,图中某条线段的长为y,如果表示y与x的函数关系的大致图象如图2所示,那么这条线段可能是
,图中某条线段的长为y,如果表示y与x的函数关系的大致图象如图2所示,那么这条线段可能是![]()
![]()
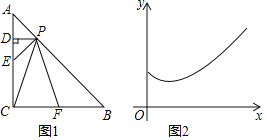
A. PDB. PEC. PCD. PF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解决问题:
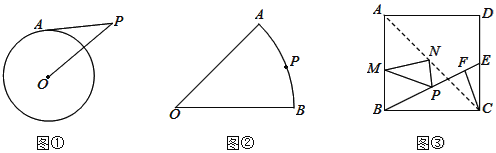
![]() 如图
如图![]() ,半径为4的
,半径为4的![]() 外有一点P,且
外有一点P,且![]() ,点A在
,点A在![]() 上,则PA的最大值和最小值分别是______和______.
上,则PA的最大值和最小值分别是______和______.
![]() 如图
如图![]() ,扇形AOB的半径为4,
,扇形AOB的半径为4,![]() ,P为弧AB上一点,分别在OA边找点E,在OB边上找一点F,使得
,P为弧AB上一点,分别在OA边找点E,在OB边上找一点F,使得![]() 周长的最小,请在图
周长的最小,请在图![]() 中确定点E、F的位置并直接写出
中确定点E、F的位置并直接写出![]() 周长的最小值;
周长的最小值;
拓展应用
![]() 如图
如图![]() ,正方形ABCD的边长为
,正方形ABCD的边长为![]() ;E是CD上一点
;E是CD上一点![]() 不与D、C重合
不与D、C重合![]() ,
,![]() 于F,P在BE上,且
于F,P在BE上,且![]() ,M、N分别是AB、AC上动点,求
,M、N分别是AB、AC上动点,求![]() 周长的最小值.
周长的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com