【题目】某商场销售一批衬衫，平均每天可售出20件，每件盈利40元
为了扩大销售，增加盈利，商场决定采取降价措施，经调查发现，若毎件衬衫每降价1元，商场平均每天可多售出2件．
若每件降价x元，每天盈利y元，求出y与x之间的关系式；
每件衬衫降价多少元时，商场每天盈利最多？盈利多少元？
课堂练加测系列答案
轻松课堂单元测试AB卷系列答案科目：初中数学 来源： 题型：
【题目】为了估计某地区供暖期间空气质量情况，某同学在20天里做了如下记录：
其中ω＜50时空气质量为优，50≤ω≤100时空气质量为良，100＜ω≤150时空气质量为轻度污染．若按供暖期125天计算，请你估计该地区在供暖期间空气质量达到良以上（含良）的天数为（ ）
污染指数（ω） | 40 | 60 | 80 | 100 | 120 | 140 |
天数（天） | 3 | 2 | 3 | 4 | 5 | 3 |
A. 75B. 65C. 85D. 100
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线y＝x﹣3与x轴、y轴分别交于点B、点C，经过B、C两点的抛物线y＝﹣x2+mx+n与x轴的另一个交点为A，顶点为P．
(1)求3m+n的值；
(2)在该抛物线的对称轴上是否存在点Q，使以C，P，Q为顶点的三角形为等腰三角形？若存在，求出有符合条件的点Q的坐标；若不存在，请说明理由．
(3)将该抛物线在x轴上方的部分沿x轴向下翻折，图象的其余部分保持不变，翻折后的图象与原图象x轴下方的部分组成一个“M“形状的新图象，若直线y＝x+b与该“M”形状的图象部分恰好有三个公共点，求b的值．
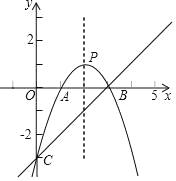
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知关于x的一元二次方程x2+（2m+1）x+m2﹣2=0．
（1）若该方程有两个实数根，求m的最小整数值；
（2）若方程的两个实数根为x1，x2，且（x1﹣x2）2+m2=21，求m的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在抛掷硬币的试验中，下列结论正确的是
A. 经过大量重复的抛掷硬币试验，可发现“正面向上”的频率越来越稳定
B. 抛掷10000次硬币与抛掷12000次硬币“正面向上”的频率相同
C. 抛掷50000次硬币，可得“正面向上”的频率为
D. 若抛掷2000次硬币“正面向上”的频率是
，则“正面向下”的频率也为
查看答案和解析>>
科目：初中数学 来源： 题型：
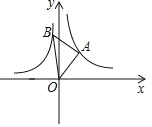
【题目】如图，在平面直角坐标系中，等腰Rt△ABO的顶点A，B分别在反比例函数y＝
（k＞0）与y＝﹣
上，且A点的横坐标为2，则k的值为（ ）
A. 
B. 
C. 1D. 1+
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若一个四位正整数s，中间两位均为3，则称这个四位正整数为“三中全会数”；若将这个“三中全会数”的个位与千位交换位置得到新的正整数记为s'，并记F（s）＝
．例如：F（4331）＝
．
（1）最小的“三中全会数”是 ；F（2331）＝ ；
（2）若“三中全会数”的个位与千位数字恰好相同，则又称这个四位正整数为“三中对称数”，若“三中全会数”x，y中x恰好是“三中对称数”，且F（x）能被11整除；F（y）﹣2F（x）＝31，求出“三中全会数”y的所有可能值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：在
中，C、D分别为BM、AM上的点，四边形ABCD内接于
，连接AC，
；
如图
，求证：弧
弧BD；
如图
，若AB为直径，
，求
值；
如图
，在的条件下，E为弧CD上一点
不与C、D重合
，F为AB上一点，连接EF交AC于点N，连接DN、DE，若
，
，
，求AN的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线l上有两动点C、D，点A、点B在直线l同侧，且A点与B点分别到l的距离为a米和b米（即图中AA′=a米，BB′=b米），且A′B′=c米，动点CD之间的距离总为S米，使C到A的距离与D到B的距离之和最小，则AC+BD的最小值为（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
