
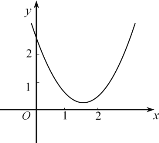
【题目】二次函数y1=ax2+bx+c(a,b,c为常数)的图象如图所示,若y1+y2=2,则下列关于函数y2的图象与性质描述正确的是:( )
A.函数y2的图象开口向上
B.函数y2的图象与x轴没有公共点
C.当x>2时,y2随x的增大而减小
D.当x=1时,函数y2的值小于0
【答案】C
【解析】
由图象开口方向及与y轴的交点可知a>0,c>2,由y1+y2=2可得y2=-ax2-bx-c+2,由-a<0可对A进行判断;根据顶点坐标方程可得出y2的最大值,由y2解析式可得y2与y轴的交点可对B进行判断;根据对称轴可对C进行判断;把x=1代入y1和y2解析式,根据y1图象可对D进行判断.综上即可得答案.
∵y1的图象开口向上,与y轴交点在(0,2)上方,
∴a>0,c>2,
∵y1+y2=2,
∴y2=-y1+2=-ax2-bx-c+2,
∵-a<0,
∴函数y2的图像开口向下,故A错误,
∴y2的最大值为![]() =-
=-![]() +2,
+2,
∵![]() <1,
<1,
∴-![]() +2>1
+2>1
∴函数y2的图像与x轴有两个交点,故B错误,
∵对称轴直线在1和2之间,图象开口向下,
∴x>2时,y2随x的增大而减小,故C正确,
∵x=1时,y1=a+b+c<2,
∴-(a+b+c)>-2
∴x=1时,y2=-a-b-c+2=-(a+b+c)+2>0,故D错误,
故选C.


科目:初中数学 来源: 题型:
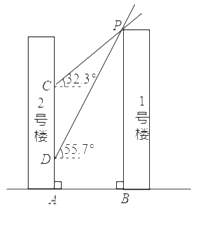
【题目】如图,![]() 号楼在
号楼在![]() 号楼的南侧,两楼高度均为
号楼的南侧,两楼高度均为![]() 楼间距为
楼间距为![]() .冬至日正午,太阳光线与水平面所成的角为
.冬至日正午,太阳光线与水平面所成的角为![]() .
.![]() 号楼在
号楼在![]() 号楼墙面上的影高为
号楼墙面上的影高为![]() ,春分日正午,太阳光线与水平面所成的角为
,春分日正午,太阳光线与水平面所成的角为![]() ,
,![]() 号楼在
号楼在![]() 号楼墙面上的影高为
号楼墙面上的影高为![]() .已知
.已知![]() .
.
(1)求楼间距![]() ;
;
(2)若![]() 号楼共
号楼共![]() 层,层高均为
层,层高均为![]() 则点
则点![]() 位于第几层? ( 参考数据:
位于第几层? ( 参考数据:![]()
![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象在第一象限交于点
的图象在第一象限交于点![]() ,与
,与![]() 轴的负半轴交于点
轴的负半轴交于点![]() ,且
,且![]() .
.
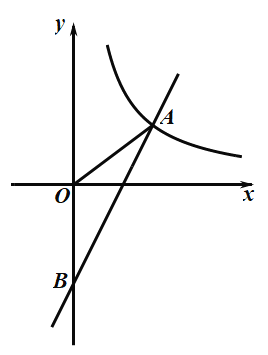
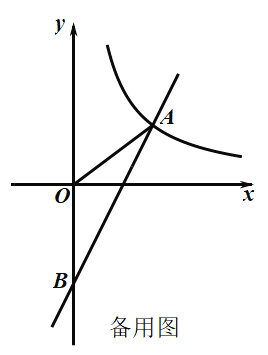
(1)求一次函数![]() 和
和![]() 的表达式;
的表达式;
(2)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 是以
是以![]() 为腰的等腰三角形,若存在,求出点
为腰的等腰三角形,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)反比例函数![]() 的图象记为曲线
的图象记为曲线![]() ,将
,将![]() 向右平移3个单位长度,得曲线
向右平移3个单位长度,得曲线![]() ,则
,则![]() 平移至
平移至![]() 处所扫过的面积是_________.(直接写出答案)
处所扫过的面积是_________.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB,
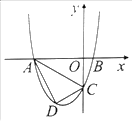
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在x轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示的是一种折叠门,已知门框的宽度AD=2米,两扇门的大小相同(即AB=CD),且AB+CD=AD,现将右边的门CDD1C1绕门轴DD1向外面旋转67°(如图2).
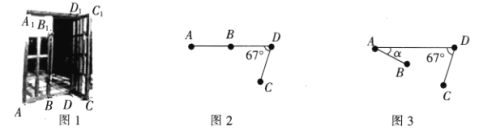
(1)求点C到AD的距离.
(2)将左边的门ABB1A1绕门轴AA1向外面旋转,设旋转角为α(如图3),问α为多少时,点B,C之间的距离最短?(参考数据:sin67°≈0.92,cos67°≈0.39,tan29.6°≈0.57,tan19.6°≈0.36,sin29.6°≈0.49)
查看答案和解析>>
科目:初中数学 来源: 题型:
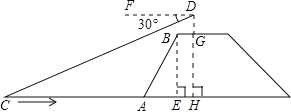
【题目】如图,兰兰站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,测得小船C的俯角是∠FDC=30°,若兰兰的眼睛与地面的距离是1.5米,BG=1米,BG平行于AC所在的直线,迎水坡的坡度i=4:3,坡高BE=8米,求小船C到岸边的距离CA的长.(参考数据:![]() ≈1.7,结果保留一位小数)
≈1.7,结果保留一位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的负半轴上,点D、M分别在边AB、OA上,且AD=2DB,AM=2MO,一次函数y=kx+b的图象过点D和M,反比例函数y=![]() 的图象经过点D,与BC的交点为N.
的图象经过点D,与BC的交点为N.
(1)求反比例函数和一次函数的解析式;
(2)若点P在直线DM上,且使△OPM的面积与四边形OMNC的面积相等,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
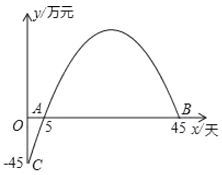
【题目】天然生物制药公司投资制造某药品,先期投入了部分资金.企划部门根据以往经验发现,生产销售中所获总利润![]() 随天数
随天数![]() (可以取分数)的变化图象如下,当总利润到达峰值后会逐渐下降,当利润下降到
(可以取分数)的变化图象如下,当总利润到达峰值后会逐渐下降,当利润下降到![]() 万元时即为止损点,则停止生产
万元时即为止损点,则停止生产
(1)设![]() ,求出最大利润是多少?
,求出最大利润是多少?
(2)在(1)的条件下,经公司研究发现如果添加![]() 名工人
名工人![]() ,在工资成本增加的情况下,总利润关系式变为
,在工资成本增加的情况下,总利润关系式变为![]() ,请研究添加
,请研究添加![]() 名工人后总利润的最大值,并给出总利润最大的方案中的
名工人后总利润的最大值,并给出总利润最大的方案中的![]() 值及生产天数.
值及生产天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明想利用所学知识测量一公园门前热气球直径的大小,如图,当热气球升到某一位置时,小明在点A处测得热气球底部点C、中部点D的仰角分别为50°和60°,已知点O为热气球中心,EA⊥AB,OB⊥AB,OB⊥OD,点C在OB上,AB=30m,且点E、A、B、O、D在同一平面内,根据以上提供的信息,求热气球的直径约为多少米?(精确到0.1m)
(参考数据:sin50°≈0.7660,cos50°≈0.6428,tan50°=1.192)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com